https://geometry.ru/olimp/2024/2024_zaoch_rus.pdf
https://geometry.ru/olimp/2024/2024_zaoch_eng.pdf

начинается заочный тур XX олимпиады им. И.Ф.Шарыгина

как обычно: 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии

Даны точки A,B,C. Построить окружность, проходящую через A и B, для которой касательные к ней из точки С образуют прямой угол.

// коллега Кноп предложил в https://www.facebook.com/groups/mathpuz

На доске нарисовали пятиугольник. Потом его стёрли, но оставили середины всех сторон. Как по этим пяти точкам восстановить пятиугольник?

📢 Лекция Григория МЕРЗОНА в это воскресенье, 10 декабря 18:00 МСК

Григорий Мерзон — сотрудник МЦНМО и Лаб. популяризации и пропаганды математики МИАН, редактор журнала «Квантик».

🔍 Геометрические неравенства

📝 Мы поговорим про геометрические неравенства. Вот два примера задач.

* Как оценить площадь фигуры, если известен ее периметр? Как уточнить оценку, если известна дополнительная информация про геометрию фигуры?

* В метро разрешается проносить только такие коробки (прямоугольные параллелепипеды), у которых сумма измерений по длине, ширине и высоте не больше 150 см. Можно ли обойти это правило, убрав запрещенную коробку внутрь разрешенной?

Рассказ предполагается элементарным. От слушателей ожидается, что они знают формулу площади круга, морально готовы (не только рисовать картинки, но и) раскрывать скобки, не боятся слова “вероятность”.

⏰ Начало в 18:00 МСК.

📌 Ссылка на Zoom.

#открытые_лекции #анонс

В остроугольном треугольнике ABC из вершин A, B, C опущены высоты в точки D, E, F соответственно. Вокруг треугольника ABC описана окружность. Прямая FE пересекает окружность в такой точке P, что F находится между P и E. Прямые BP и DF пересекаются в точке Q. Доказать, что, если PE=DE, DP || CQ

Муниципальный этап, 2023 год, Ставропольский край, 11 класс

https://polit.ru/articles/publichnye-lektsii/grisha-perelman-yabloko-i-bublik-2015-03-11/

https://youtu.be/4a7UeLRtxXY

популярный рассказ Сергея Дужина про топологию, гипотезу Пуанкаре и всё такое

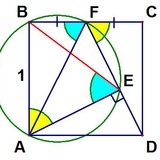
Даны окружность и прямая. Построить квадрат как на рисунке.

// задачку рассказал коллега Швецов на семинаре сегодня

еще с вчерашнего семинара:

- посмотрите на картинку, сформулируйте и докажите утверждение

- подумайте про эту картинку еще и извлеките из нее, что три линии типа пунктирной пересекаются в одной точке…

- …и заодно какое-нибудь утверждение про эту точку

https://youtu.be/Gp8XaGRaqCY

https://geometry.ru/hom.html

мини-курс Д.Швецова про гомотетию и рассказ про это на семинаре учителей в МЦНМО

Задача про квадрат с простого тура прошедшей на выходных геометрической олимпиады им. Ясинского. Автор: Матвей Курский.

Источник: https://www.facebook.com/share/1MHmPaFkLEDfhxWF/?mibextid=o8wo0F

Очень симпатичное наблюдение от Михаила Сидоренко

Олимпиада Ясинского 2023, Задача 4, 11 класс.

Точка C выбирается на окружности с диаметром AB. Точки Р и Q на гипотенузе треугольника ABC таковы, что AC=AQ, BC=BР. Докажите, что прямые Эйлера треугольников CPQ, когда C меняется, проходят через фиксированную точку.

Выпуклый четырехугольник ABCD описан около окружности ω. Пусть PQ — диаметр ω, перпендикулярный AC. Пусть прямые BP и DQ пересекаются в точке X, а прямые BQ и DP — в точке Y. Доказать, что точки X и Y лежат на прямой AC.

>>
электрон тетраэдр так же неисчерпаем, как атом треугольник (Ленин Руденко).
>>

Даня Руденко занимался алгебраической геометрией, и по ходу открыл новое тождество для тетраэдров (по ссылке вполне mesmerizing story об этом). После долгих поисков он обнаружил похожее тождество в старинном журнале The Educational Times.

Потом он же сотоварищи сделал сайт с геометрическими задачками из старых журналов.

На сайте тысячи старинных задач с прикрученным поиском. Красота! Практически склеил двух столетий позвонки (в хорошем смысле).

Если есть предложения как улучшить сайт с задачами: предлагайте!

📝 Запись лекции про геометрические неравенства

🎤 Неделю назад Григорий Мерзон прочел очень интересную лекцию про изопараметрическое неравенство и формулу Штейнера.

📚 Все материалы лекции выложены на страничке докладчика. Там вы найдёте слайды с лекции, ссылки на популярные книги и статьи в Кванте, видео 3Blue1Brown и серьезный обзор по теме.

#открытые_лекции #YouTube

Прямая касается гиперболы. Доказать, что точка касания — середина отрезка, высекаемого на прямой асимптотами.

один из способов решить задачу выше — при помощи гиперболического поворота перевести точку касания на ось гиперболы (где утверждение очевидно из симметрии)

заодно будет видно, что все касательные отсекают от асимптот треугольники одной и той же площади

(ср. с тем, что для пары концентрических окружностей касательная к внутренней всегда делится точкой касания пополам и всегда отсекает одну и ту же площадь)

про гиперболические повороты (и немножко про параболические повороты) можно прочитать в статье https://www.mathnet.ru/rus/kvant565 Дворянинова и Кожевникова в Кванте

вокруг каждого из лучей пятиконечной звезды описали по окружности

доказать, что их точки пересечения лежат на одной окружности