Треугольник вписан в параболу так, что биссектриса его угла перпендикулярна оси параболы. Доказать, что середина медианы (из того же угла) лежит на оси.

// Задача с проходившей сейчас олимпиады «Ассара». Близкие вещи здесь обсуждались — но хотел бы узнать: а есть аналог с окружностью вместо параболы?

Даны 4 точки. Построить проходящую через них параболу. Сколько, кстати, таких парабол?

// Задача из обсуждений в группе. Строить предлагается либо фокус и директрису циркулем и линейкой, либо прямо параболу (параболы) в геогебре.

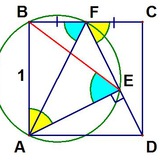
Придумал задачку. Дан треугольник ABC с вершинами в узлах сетки (см. рисунок). Как с помощью только линейки построить какую-нибудь его биссектрису?
Подсказка: биссектрису угла B.

Опрос ↑↑

понравилась статья П.Кожевникова с разными точками зрения на изогональное сопряжение, https://www.mathnet.ru/rus/kvant1354 (Квант №1 за 2016 год)

для привлечения внимания — вот несколько картинок оттуда

Углы A и C четырехугольника ABCD равны. Доказать, что середина AC и проекции D на AB, BC, AC лежат на одной окружности.

Еще одна точка зрения на изогональное сопряжение: точки сопряжены <=> это фокусы вписанной в треугольник коники.

(Такое обобщение того, что центр [вне]вписанной окружности изогонально сопряжен сам себе.)

В частности, описанная окружность есть ГМТ фокусов касающихся сторон треугольника парабол — картинки на эту тему здесь уже были, https://tttttt.me/geometrykanal/1826

// Это тж. по касательной к https://tttttt.me/olympgeom/1027

картинки по выходным: теорема Наполеона и ее родствениики из свежего Квантика, https://kvantik.com/issue/pdf/2023-11_sample.pdf

#22 (Теорема Харта)

Доказать, что существует окружность, касающаяся четырех серых окружностей

📢 Лекция Григория Папаянова в это воскресенье, 19 ноября, в 17:00

Григорий - математик, выпускник матфака ВШЭ, phd университета Northwestern, работает в университете Хайфы.

Он расскажет про такую проблему: когда два многогранника можно разрезать на одинаковые части? Это тему у нас уже затрагивал Сергей Буфеев, можете почитать пост один и два.

🔍 Разрезания многогранников и инвариант Дена

📝 Возьмите треугольник. Попробуйте его разрезать ножницами на несколько частей и потом сложить из этих частей квадрат. Если у вас получилось, вы, можно считать, доказали теорему Бойяи-Гервина (первоначально доказанную, видимо, Вильямом Уоллесом в 1807 году). Третья проблема из знаменитого списка Гильберта спрашивает, можно ли как-нибудь аналогично разрезать тетраэдр и составить из кусочков куб? Макс Ден, ученик Гильберта, опубликовал отрицательное решение этой проблемы, примерно в то же самое время, как Гильберт свой список обнародовал.
Решение это состояло в построении интересного численного инварианта многогранника, не меняющегося при операции разрезания на кусочки и пересобирания. Мы обсудим определение инварианта Дена и посмотрим, как именно оно мешает нам сложить из тетраэдра куб.

Для понимания рассказа никаких предварительных знаний, в общем, не требуется (но ножницы приносите свои).

⏰ Начало в 18:00 МСК.

📌 Ссылка на зум.

#открытые_лекции #анонс

Точку Торричелли треугольника соединили с вершинами. В трех получившихся треугольниках провели прямые Эйлера. Доказать, что они проходят через одну точку.

// задачку рассказал Р.К.Гордин сегодня

Чертеж специально не рисую, потому что в процессе решения его понадобится перерисовать.

Источник: основной тур Турнира Городов этого года https://www.turgor.ru/problems/

1) На плоскости выбраны 4 точки в общем положении. Для каждых 3 из них проведем окружность девяти точек соответствующего треугольника. Доказать, что 4 полученные окружности пересекаются в одной точке.

2) На плоскости выбраны 4 прямые в общем положении. Для каждых 3 из них проведем описанную окружность соответствующего треугольника. Доказать, что 4 полученные окружности пересекаются в одной точке.

На окружности лежат 4 точки. Для каждых 3 из них отметим ортоцентр соответствующего треугольника. Доказать, что получившийся четырехугольник равен исходному.

Доказать, что правильном 12-угольнике есть отличная от центра точка, в которой пересекаются 4 диагонали.

(Можно порисовать картинки и придумать решение совсем минимальными средствами, которое доступно и тем, кто только начал изучать геометрию.)

Для тех, кто уже изучил 12-угольник — бонусный вопрос:

Бывает ли так, что в правильном многоугольнике три диагонали пересекаются не на одной из осей симметрии?

в качестве подсказки — разбиение правильного 12-угольника на правильный 6-угольник, квадраты и правильные треугольники

см. также небольшую статью про правильный 12-угольник в Квантике, https://old.kvantik.com/art/files/pdf/2014-07.18-19.pdf