Forwarded from Фулл и точка
This media is not supported in your browser
VIEW IN TELEGRAM
#красота_спасет_мир #ЮМТ
Команда авторов канала сейчас на Южном математическом турнире 🙂
Мы будем держать вас в курсе событий 😉 Ожидается очень много крутых геометрий 🔥
А вот и первая — своеобразный тест на профессионала с довольно изящной формулировкой от Павла Александровича 🤗
Задача. Трапеция 𝐴𝐵𝐶𝐷 (𝐴𝐵 ‖ 𝐶𝐷) вписана в окружность Ω. Рассмотрим всевозможные окружности Γ, которые касаются отрезка 𝐶𝐷 и той дуги 𝐶𝐷 окружности Ω, что не содержит точек 𝐴 и 𝐵. Пусть Γ касается сторон некоторого угла ∠𝐴𝑃𝐵 в точках 𝐾 и 𝐿 соответственно. Докажите, что сумма 𝐴𝐾 + 𝐵𝐿 постоянна (то есть не зависит от выбора окружности Γ).
На командной олимпиаде в старшей лиге была еще одна прикольная геометрия от нашего подписчика Вовы Конышева. С ней справилась всего одна команда! 🤯
Условие и картинку к сложной задачке вы сможете найти в комментариях к посту 👇
Там же лежит неподвижная картинка к задаче от Павла Александровича 💜
Добавляйтесь в наш чат, чтобы ничего не пропустить!
Команда авторов канала сейчас на Южном математическом турнире 🙂
Мы будем держать вас в курсе событий 😉 Ожидается очень много крутых геометрий 🔥
А вот и первая — своеобразный тест на профессионала с довольно изящной формулировкой от Павла Александровича 🤗
Задача. Трапеция 𝐴𝐵𝐶𝐷 (𝐴𝐵 ‖ 𝐶𝐷) вписана в окружность Ω. Рассмотрим всевозможные окружности Γ, которые касаются отрезка 𝐶𝐷 и той дуги 𝐶𝐷 окружности Ω, что не содержит точек 𝐴 и 𝐵. Пусть Γ касается сторон некоторого угла ∠𝐴𝑃𝐵 в точках 𝐾 и 𝐿 соответственно. Докажите, что сумма 𝐴𝐾 + 𝐵𝐿 постоянна (то есть не зависит от выбора окружности Γ).
На командной олимпиаде в старшей лиге была еще одна прикольная геометрия от нашего подписчика Вовы Конышева. С ней справилась всего одна команда! 🤯
Условие и картинку к сложной задачке вы сможете найти в комментариях к посту 👇
Там же лежит неподвижная картинка к задаче от Павла Александровича 💜
Добавляйтесь в наш чат, чтобы ничего не пропустить!
❤10👍5
Задача о которой идет речь в посте выше
❤2
Forwarded from Фулл и точка. Обсуждение
Задача. Дан треугольник 𝐴𝐵𝐶, пусть 𝑄 — проекция ортоцентра на медиану треугольника 𝐴𝐵𝐶, выходящую из 𝐴. На отрезке 𝐵𝐶 выбрана произвольная точка 𝑇. Прямая 𝐴𝑇 пересекает окружности (𝑄𝐴𝐵) и (𝑄𝐴𝐶) повторно в точках 𝐵′, 𝐶′ соответственно. Прямые 𝐵𝐵′ и 𝐶𝐶′ пересекаются в точке 𝐾. На прямой 𝐴𝐾 выбрана точка 𝐿, отличная от 𝐴, так что 𝑇𝐴 = 𝑇𝐿. Докажите, что прямая 𝑇𝐿 касается окружности (𝑄𝐵′𝐶′).
🔥9❤3👎2
Выше предлагалась примерно такая задача: смотрим на точки, из которых пара окружностей видна под данным углом, проводим биссектрисы этих углов, доказать, что все они касаются какой-то окружности (см. рис.).
Хочу поделиться спойлером, как решатьпочти любую задачу: если сразу идей нет, рассмотреть более простого родственника.
Выродим окружности из условия в точки. Что получится? Из точки P отрезок XY виден под фиксированным углом — то есть P лежит на дуге окружности. А биссектрисаделит оставшуюся дугу пополам… то есть всевозможные биссектрисы в данном случае проходят через фиксированную точку.
Чтобы связать это с исходной задачей, можноотметить центры окружностей из условия и ———
Хочу поделиться спойлером, как решать
Выродим окружности из условия в точки. Что получится? Из точки P отрезок XY виден под фиксированным углом — то есть P лежит на дуге окружности. А биссектриса
Чтобы связать это с исходной задачей, можно
🔥8
Forwarded from Фулл и точка
#ЮМТ
Предлагаем вашему вниманию замечательную задачку от нашего подписчика Кирилла Бельского 🔥
Задача прекрасна тем, что не только имеет красивое и не требующее особых знаний геометрическое решение, но и тем, что обученнные люди в ней смогут разглядеть факт проконики 🤩
Однако, будьте аккуратнее — на профессиональном пути решения можно споткнуться, как случилось сегодня на матбою, где одна из команд, почти полностью рассказав решение, получила за него всего два балла 🤯
Задача. Дан выпуклый четырёхугольник 𝐴𝐵𝐶𝐷, диагонали которого пересекаются в точке 𝑂. Внутри треугольников 𝑂𝐴𝐷 и 𝑂𝐵𝐶 выбраны точки 𝑋 и 𝑌 соответственно так, что ∠𝑂𝐵𝑌 = ∠𝑋𝐴𝐷, ∠𝑂𝐷𝑋 = ∠𝐵𝐶𝑌 и точки 𝑂, 𝑋, 𝑌 лежат на одной прямой. Оказалось,что точки 𝐴, 𝐵, 𝐶, 𝐷 не лежат на одной окружности. Докажите, что 𝐶𝑌 ‖ 𝐴𝑋.
Предлагаем вашему вниманию замечательную задачку от нашего подписчика Кирилла Бельского 🔥
Задача прекрасна тем, что не только имеет красивое и не требующее особых знаний геометрическое решение, но и тем, что обученнные люди в ней смогут разглядеть факт про
Однако, будьте аккуратнее — на профессиональном пути решения можно споткнуться, как случилось сегодня на матбою, где одна из команд, почти полностью рассказав решение, получила за него всего два балла 🤯
Задача. Дан выпуклый четырёхугольник 𝐴𝐵𝐶𝐷, диагонали которого пересекаются в точке 𝑂. Внутри треугольников 𝑂𝐴𝐷 и 𝑂𝐵𝐶 выбраны точки 𝑋 и 𝑌 соответственно так, что ∠𝑂𝐵𝑌 = ∠𝑋𝐴𝐷, ∠𝑂𝐷𝑋 = ∠𝐵𝐶𝑌 и точки 𝑂, 𝑋, 𝑌 лежат на одной прямой. Оказалось,что точки 𝐴, 𝐵, 𝐶, 𝐷 не лежат на одной окружности. Докажите, что 𝐶𝑌 ‖ 𝐴𝑋.
❤9👍1
Авторское решение задачи выше: Пусть AX и BY пересекаются в точке E. Тогда из углов видно, что точки A,B,D,E лежат на одной окружности. Пусть CY и DX пересекаются в точке F. Тогда аналогично из углов видно, что точки C,B,D,F лежат на одной окружности. А еще если внимательно посмотреть, то можно увидеть, что для точек ABCDEF выполнена теорема Паскаля. А значит точки A,B,C,D,E,F лежат на одной конике, которая не является окружностью по условию! Осталось применить лемму Фусса для коник (2 картинка).
👍15❤2🔥2👎1
Forwarded from Фулл и точка
#геом_разминка #ЮМТ
Начнем это утро с прикольной задачки со вчерашнего конкурса капитанов 🙂
Задача. Существует ли такой неравнобедренный треугольник, что его можно двумя способами разрезать на два равнобедренных треугольника?
Всем добра 🤗
Начнем это утро с прикольной задачки со вчерашнего конкурса капитанов 🙂
Задача. Существует ли такой неравнобедренный треугольник, что его можно двумя способами разрезать на два равнобедренных треугольника?
Всем добра 🤗
❤23👍2
Forwarded from Геометрия с Ниловым
В окружность вписан прямоугольник ABCD. По прямой AD движется точка M. Перпендикуляры к отрезкам MB и MC, восстановленные в точках B и C, пересекаются в точке N. Докажите, что точка N движется по параболе, касающейся окружности в точках B и C.
Анимация в geogebra:
https://www.geogebra.org/classic/bethsmt3
Анимация в geogebra:
https://www.geogebra.org/classic/bethsmt3
❤11👍2😐2
на картинке мозаика, глядя на которую можно понять, как правильный 8-угольник разрезать на части и сложить из них квадрат
подробности и история — на сайте Мат. Этюдов, https://etudes.ru/models/square-octagon/
ранее на тему разрезаний и паркетов: https://tttttt.me/geometrykanal/1508 https://tttttt.me/geometrykanal/1509
подробности и история — на сайте Мат. Этюдов, https://etudes.ru/models/square-octagon/
ранее на тему разрезаний и паркетов: https://tttttt.me/geometrykanal/1508 https://tttttt.me/geometrykanal/1509
❤17👍3🔥3
Forwarded from Геометрия от Волчкевича
Три квадрата
Легко заметить, что эти три задачи имеют много общего. Для решения первой хватит знаний 7 класса, вторая по силам уже восьмикласснику, а третью лучше решать в 9 классе. Получилась вот такая серия задачек «на вырост».
Как обычно, в комментариях пишите свои ответы.
Легко заметить, что эти три задачи имеют много общего. Для решения первой хватит знаний 7 класса, вторая по силам уже восьмикласснику, а третью лучше решать в 9 классе. Получилась вот такая серия задачек «на вырост».
Как обычно, в комментариях пишите свои ответы.
❤16👏1
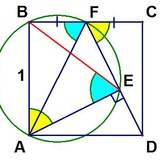
В треугольнике АВС: ∠B=110°, ∠С=30°, О — центр описанной окружности. Биссектриса внешнего угла А пересекает прямую ВС в точке L. Чему равен ∠AOL?
Anonymous Quiz
3%
10°
5%
15°
10%
20°
6%
25°
24%
30°
9%
35°
12%
40°
5%
45°
9%
60°
17%
среди предложенных ответов нет правильного
1💯10❤5🌚3👍1🔥1
Решение задачи выше.
❤5
Forwarded from Математика + анимации
This media is not supported in your browser
VIEW IN TELEGRAM
❤11👍5🕊3🔥1
в МЦНМО кроме обычных математических кружков иногда бывают кружки по геометрии
в этом году — геометрия для 9- и 10-классников по средам, https://mccme.ru/circles/mccme/2025/geom/
вот, например, ниже задача для привлечения внимания
в этом году — геометрия для 9- и 10-классников по средам, https://mccme.ru/circles/mccme/2025/geom/
вот, например, ниже задача для привлечения внимания
🔥6❤1
Forwarded from Мария
(10-2, устный тур олимпиады Шарыгина 2021 года). Авторское решение данной задачи использует свойства гармонических четверок , но есть и более простое решение, которое мы обсудим на кружке.
В неравнобедренном треугольнике ABC точки A0, B0, C0 - середины сторон BC, CA, AB. Биссектриса угла C пересекает прямые A0C0 и B0C0 в точках B1 и A1. Докажите, что прямые AB1, BA1 и A0B0 пересекаются в одной точке.
В неравнобедренном треугольнике ABC точки A0, B0, C0 - середины сторон BC, CA, AB. Биссектриса угла C пересекает прямые A0C0 и B0C0 в точках B1 и A1. Докажите, что прямые AB1, BA1 и A0B0 пересекаются в одной точке.
❤8🔥1
Forwarded from Олимпиадная геометрия
axial_symmetry.pdf
167.4 KB
продолжаю публиковать листочки для начинающих геометров. вот листик про осевую симметрию, в котором знать почти ничего и не надо.
❤4👍1🔥1
Forwarded from Непрерывное математическое образование
на рисунке правильный треугольник сложен из одинаковых красных прямоугольных треугольников и одинаковых зеленых равнобедренных треугольников
во сколько раз площадь большого треугольника больше площади зеленого?
// доступная начинающим задача М.Евдокимова с проходившего вчера Турнира Ломоносова
во сколько раз площадь большого треугольника больше площади зеленого?
// доступная начинающим задача М.Евдокимова с проходившего вчера Турнира Ломоносова
👍9❤7🔥1