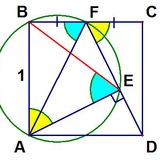
На отрезке АВ=2 взяли точку С. На отрезках АС и ВС с разных сторон относительно АВ построили квадраты АСDE и CBFG. М и N — их центры соответственно. Чему равна площадь четырёхугольника MNBD?
#начинающим
#начинающим
🔥13❤1👍1
Продолжаем. Вот еще мой листик (хотя скорее два) про прямую Штейнера и прямую Симсона. Опять же может не самый хороший)
🤔5❤1👍1
👍8❤2🤩1
Задача Егора Бакаева с Турнира Городов (базовый тур, 8-9 класс, осень 2024)
Дан описанный пятиугольник 𝐴𝐵𝐶𝐷𝐸. Центр его вписанной окружности лежит на диагонали 𝐴𝐶. Докажите, что 𝐴𝐵 + 𝐵𝐶 > 𝐶𝐷 + 𝐷𝐸 + 𝐸𝐴
Картинку мы взяли в канале Фулл и точка
А тут остальные задачи этого тура
Дан описанный пятиугольник 𝐴𝐵𝐶𝐷𝐸. Центр его вписанной окружности лежит на диагонали 𝐴𝐶. Докажите, что 𝐴𝐵 + 𝐵𝐶 > 𝐶𝐷 + 𝐷𝐸 + 𝐸𝐴
Картинку мы взяли в канале Фулл и точка
А тут остальные задачи этого тура
1❤8🔥6😁5
А у 10-11 классов на Тургоре была задача Михаила Евдокимова, тоже прекрасная.
В равностороннем треугольнике ABC проведены отрезки ED и GF, так что образовались два равносторонних треугольника ADE и GFC со сторонами 1 и 100 (точки E и G лежат на стороне AC).
Отрезки EF и DG пересекаются в точке O, причём ∠EOG = 120°.
Чему равна сторона треугольника ABC?
В равностороннем треугольнике ABC проведены отрезки ED и GF, так что образовались два равносторонних треугольника ADE и GFC со сторонами 1 и 100 (точки E и G лежат на стороне AC).
Отрезки EF и DG пересекаются в точке O, причём ∠EOG = 120°.
Чему равна сторона треугольника ABC?
❤10
Forwarded from Быстрые задачки по математике (Наталья Нетрусова)
Даны прямая a и точка А вне неё. Вася выбирает четыре точки на прямой а, и соединяет их отрезками с точкой А. Какое наибольшее количество равнобедренных треугольников может у него получиться?
Anonymous Quiz
2%
0
5%
1
25%
2
7%
3
22%
4
6%
5
24%
6
2%
7
3%
8
4%
Здесь нет правильного ответа
🤷♂9👍8🔥5❤3🌚1
На стороне BC треугольника выбирают точку D. B треугольники ABD и ACD вписывают окружности. Их общая внешняя касательная пересекает AD в точке K. Доказать, что длина AK не зависит от выбора точки D.
// Задача И.Ф.Шарыгина на ММО-1994 с сегодняшнего семинара. Подходит начинающим — никакие знания сверх школьной программы не требуются (но надо не полениться)
// Задача И.Ф.Шарыгина на ММО-1994 с сегодняшнего семинара. Подходит начинающим — никакие знания сверх школьной программы не требуются (но надо не полениться)
1❤8👍5
В прямоугольный треугольник вписана окружность. Через точку её касания с катетом проведён перпендикуляр к хорде, соединяющий другие две точки касния. Доказать, что этот перпендикуляр высекает на катете отрезок, равный радиусу вписанной окружности.
// Задача М.А.Волчкевича на ММО-2007 со вчерашнего семинара. Тоже не требует никаких знаний (но придумать решение не так просто). В комментариях есть обобщение
// Задача М.А.Волчкевича на ММО-2007 со вчерашнего семинара. Тоже не требует никаких знаний (но придумать решение не так просто). В комментариях есть обобщение
❤17👍3
параболу y=-x² пересекают всевозможными параболами вида y=x²+ax+b, проходящими через фиксированную точку
доказать, что всевозможные общие хорды этих парабол проходят через фиксированную точку
// задача П.Кожевникова с заканчивающейся сейчас олимпиады «Ассара»; все задачи — https://tttttt.me/matheduks/31
доказать, что всевозможные общие хорды этих парабол проходят через фиксированную точку
// задача П.Кожевникова с заканчивающейся сейчас олимпиады «Ассара»; все задачи — https://tttttt.me/matheduks/31
👍17
Forwarded from Повышение квалификации по математике
#семинары
❗️Семинар учителей математики в МЦНМО.
Д.Г.Мухин, Д.В.Швецов. Вписанная и вневписанная окружность.
❗️Семинар учителей математики в МЦНМО.
Д.Г.Мухин, Д.В.Швецов. Вписанная и вневписанная окружность.
YouTube
Д.Г.Мухин, Д.В.Швецов. Вписанная и вневписанная окружность
Семинар учителей математики, 10.10.2024
https://mccme.ru/nir/seminar/
https://mccme.ru/nir/seminar/
🥰13😁3👍2🔥1😱1
Forwarded from Ботаем геому
Приглашаю всех принять участие в устной олимпиаде Лицея НИУ ВШЭ по геометрии!
Олимпиада проводится для учеников 8-11 классов. Интересные задачи найдутся как для начинающих, так и для опытных геометров.
Олимпиада состоится 27 октября по адресу: ул. Солянка 14А, стр.1. Начало олимпиады в 10.00.
Для участия необходима предварительная регистрация: https://docs.google.com/forms/d/e/1FAIpQLSeYRBtcir_X2sfYnwOCrHcMahrgC2VXAAEcQC614jni048q5w/viewform?usp=sf_link
Регистрация открыта до 26 октября.
Олимпиада проводится для учеников 8-11 классов. Интересные задачи найдутся как для начинающих, так и для опытных геометров.
Олимпиада состоится 27 октября по адресу: ул. Солянка 14А, стр.1. Начало олимпиады в 10.00.
Для участия необходима предварительная регистрация: https://docs.google.com/forms/d/e/1FAIpQLSeYRBtcir_X2sfYnwOCrHcMahrgC2VXAAEcQC614jni048q5w/viewform?usp=sf_link
Регистрация открыта до 26 октября.
❤6👍2
Forwarded from Фулл и точка
#геом_разминка
Представляем вам задачу, которая вчера предлагалась на математической регате⛵️ )
Задача. Через точку 𝑀, лежащую внутри окружности и отличную от её центра, проведены три хорды так, что угол между каждыми двумя соседними равен 60°. Образовалось шесть отрезков, у которых один конец лежит на окружности, а другой в точке 𝑀. Докажите, что сумма длин трёх отрезков, взятых через один, равна сумме длин других трёх отрезков.
Желаем вам успеть всё запланированное 😎!
Представляем вам задачу, которая вчера предлагалась на математической регате
Задача. Через точку 𝑀, лежащую внутри окружности и отличную от её центра, проведены три хорды так, что угол между каждыми двумя соседними равен 60°. Образовалось шесть отрезков, у которых один конец лежит на окружности, а другой в точке 𝑀. Докажите, что сумма длин трёх отрезков, взятых через один, равна сумме длин других трёх отрезков.
Желаем вам успеть всё запланированное 😎!
Please open Telegram to view this post
VIEW IN TELEGRAM
🔥15❤4👍1
Внутри окружности расположен а) правильный б) равносторонний многоугольник. Каждую его сторону продлевают в обе стороны до окружности — появляется по два новых отрезка. Доказать, что если новые отрезки покрасить в красный и синий цвета в естественном порядке, то сумма длин красных отрезков будет равна сумме синих.
// подниму из комментариев обобщение предыдущей задачи
// подниму из комментариев обобщение предыдущей задачи
🔥8❤1
Давид Бродский написал хорошие посты про инверсию. Всем рекомендую. Пост 1, Пост 2. А ну да в комментариях написали еще уровни. Но я бы сказал, что есть только еще один уровень. Он заключается в том, что инверсия является изогональным сопряжением относительно некоторого треугольника. Треугольник немного необычный правда. Две вершины у него комплексные... Но зато это позволяет расширить инверсию на комплексные точки, а еще наверное не надо доказывать, что инверсия сохраняет двойные отношения. Но к сожалению такой взгляд не очень помогает в задачах, поэтому знать необязательно)
🔥17❤6👍3
рассматривают всевозможные пунктирные окружности, касающиеся двух данных (внутренним образом)
доказать, что концы возникающих красных хорд лежат на одной окружности
( задача П.Кожевникова на позавчерашнем Турнире городов; все задачи: https://turgor.ru/problems/46/os-46-sl-avt.pdf )
доказать, что концы возникающих красных хорд лежат на одной окружности
( задача П.Кожевникова на позавчерашнем Турнире городов; все задачи: https://turgor.ru/problems/46/os-46-sl-avt.pdf )
❤14👍2
Forwarded from Задача дня (Александр Макаренко)
Разминка дня №1
С этого дня команда администраторов будет делать почти каждый день разминки (простые задачи для всех, чтобы разбавить тот ужас, который постится здесь обычно. Обычные посты никуда не денутся)
С этого дня команда администраторов будет делать почти каждый день разминки (простые задачи для всех, чтобы разбавить тот ужас, который постится здесь обычно. Обычные посты никуда не денутся)
👍22🔥8❤3🤷♂2