#красота_спасет_мир #ЮМТ

Команда авторов канала сейчас на Южном математическом турнире 🙂

Мы будем держать вас в курсе событий 😉 Ожидается очень много крутых геометрий 🔥

А вот и первая — своеобразный тест на профессионала с довольно изящной формулировкой от Павла Александровича 🤗

Задача. Трапеция 𝐴𝐵𝐶𝐷 (𝐴𝐵 ‖ 𝐶𝐷) вписана в окружность Ω. Рассмотрим всевозможные окружности Γ, которые касаются отрезка 𝐶𝐷 и той дуги 𝐶𝐷 окружности Ω, что не содержит точек 𝐴 и 𝐵. Пусть Γ касается сторон некоторого угла ∠𝐴𝑃𝐵 в точках 𝐾 и 𝐿 соответственно. Докажите, что сумма 𝐴𝐾 + 𝐵𝐿 постоянна (то есть не зависит от выбора окружности Γ).

На командной олимпиаде в старшей лиге была еще одна прикольная геометрия от нашего подписчика Вовы Конышева. С ней справилась всего одна команда! 🤯

Условие и картинку к сложной задачке вы сможете найти в комментариях к посту 👇
Там же лежит неподвижная картинка к задаче от Павла Александровича 💜

Добавляйтесь в наш чат, чтобы ничего не пропустить!

#ЮМТ

Предлагаем вашему вниманию замечательную задачку от нашего подписчика Кирилла Бельского 🔥

Задача прекрасна тем, что не только имеет красивое и не требующее особых знаний геометрическое решение, но и тем, что обученнные люди в ней смогут разглядеть факт про коники 🤩

Однако, будьте аккуратнее — на профессиональном пути решения можно споткнуться, как случилось сегодня на матбою, где одна из команд, почти полностью рассказав решение, получила за него всего два балла 🤯

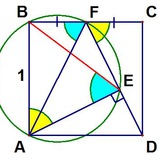
Задача. Дан выпуклый четырёхугольник 𝐴𝐵𝐶𝐷, диагонали которого пересекаются в точке 𝑂. Внутри треугольников 𝑂𝐴𝐷 и 𝑂𝐵𝐶 выбраны точки 𝑋 и 𝑌 соответственно так, что ∠𝑂𝐵𝑌 = ∠𝑋𝐴𝐷, ∠𝑂𝐷𝑋 = ∠𝐵𝐶𝑌 и точки 𝑂, 𝑋, 𝑌 лежат на одной прямой. Оказалось,что точки 𝐴, 𝐵, 𝐶, 𝐷 не лежат на одной окружности. Докажите, что 𝐶𝑌 ‖ 𝐴𝑋.

#геом_разминка #ЮМТ

Начнем это утро с прикольной задачки со вчерашнего конкурса капитанов 🙂

Задача. Существует ли такой неравнобедренный треугольник, что его можно двумя способами разрезать на два равнобедренных треугольника?

Всем добра 🤗