Прочитал про теорему Дена о разрезании: если прямоугольник можно разрезать на квадраты, то отношение его сторон рационально. Интуитивно это кажется логичным, но доказать не так уж и просто. Обратное утверждение тривиально: если отношение сторон рационально и скажем равно p/q, то увеличив масштаб в q раз, получим прямоугольник с целыми сторонами, который можно разрезать на квадраты 1x1.

Линейная алгебра помогает построить простые и красивые доказательства:

Отношение длин сторон прямоугольника W,H иррационально - это то же, что "W,H линейно независимы как векторы в пространстве R над Q". Это в свою очередь значит, что существует Q-линейная функция f:R->R, так, что f(W) и f(H) - любые удобные нам значения.

Для любой Q-линейной функции f определим f-площадь прямоугольника со сторонами A,B как f(A)*f(B). Тогда легко увидеть, что при разрезании прямоугольника на другие прямоугольники f-площадь целого равна сумме f-площади частей (это очевидно при разрезании одного прямоугольника на два, и к повторению этого можно свести любое разрезание, если сделать из него "сетку", продлив все внутренние линии до краев).

Как ни странно, доказательство почти закончено. f-площадь любого квадрата равна f(A)*f(A), то есть неотрицательна. Отсюда f-площадь любого прямоугольника размером W:H, разрезанного на квадраты, неотрицательна. Но если W/H не рационально, то мы можем выбрать такую f, что f(W)=1, f(H)=-1, и его f-площадь равна -1, это противоречие.

Другое доказательство с помощью линейной алгебры вместо f-площади пользуется тензорным произведением R@R. Если стороны прямоугольника w,h линейно независимы, то {w,h} можно продлить до базиса, и поэтому ясно, что в R@R линейно независимы также векторы w@w, w@h, h@w, h@h. С другой стороны, если прямоугольник разбит на квадраты, то w@h является суммой членов вида a@a (доказательство аналогично примеру с площадью). Это значит, что изоморфизм в R@R, который меняет координаты местами, одновременно переводит w@h в h@w и оставляет неизменным, т.е. w@h = h@w, а это противоречит их независимости.

Еще есть красивое доказательство с помощью гармонических функций на конечных графах (второе в этой заметке). А в древней книжке Яглома "Как разрезать квадрат?" (1968) есть элементарное доказательство через систему уравнений, связывающих длины сторон.

P.S. Вспоминается также замечательная статья "Fourteen proofs of a result about tiling a rectangle", где дается много доказательство похожего, но другого по сути утверждения: что если прямоугольник разрезан на прямоугольники и у каждого внутренного прямоугольника хотя бы одна из сторон - целое число, то и у всего прямоугольника тоже хотя бы одна из сторон целая.

По наводке Бори Трушина вот вам трэш-теорема. Пользуйтесь и не благодарите! Такого в школе и правда не расскажут!

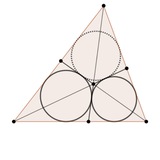
доказать, что большой четырехугольник описанный

молодцы!)

условие было такое

Преподаватели Дабромат продолжают делать крутые летние активности для вас! Для тех, кому требуется погружение в конкретную тему, а не последовательная прокачка навыков, как на летних курсах, мы подготовили линейку спецкурсов.

Что же такое спецкурс?

Это интенсивная неделя занятий, на которой подробно рассматривается одна или несколько смежных тем. Спецкурсы, как и ступени, будут разного уровня в зависимости от текущих знаний участников.

➤ «Вокруг малой теоремы Ферма, порядков чисел и леммы об уточнении показателя»

Преподаватель — Бибиков Павел Витальевич.

Каждый знает Малую теорему Ферма. Спецкурс посвящен ее уточнениям и применениям в олимпиадных задачах по теории чисел.

Занятия проводятся 24-30 июня.

➤ «Топологический путь к Вейерштрассу»

Преподаватель — Волкова Алиса Алексеевна.

Мы познакомимся с новым для многих разделом математики — топологией, в простом понимании — науке о геометрических и не только свойствах различных нестандартных объектов. Мы затронем лишь малую её часть — изучим некоторые свойства функций и отображений, но этого нам хватит, чтобы доказать теорему Вейерштрасса, теорему, которая часто помогает формализовать решение неравенств и немного модифицировать метод Штурма, что поможет применять его в более широком классе задач.

➤ «Открытая неделя по барицентрам» 1 часть

Преподаватель — Бахарев Федор Львович.

Спецкурс посвящен мощному методу решения геометрических задач — счету в барицентрических координатах.

Состоит из двух частей: подготовительной открытой недели и недельного интенсива. На открытой неделе мы кратко вспомним основные понятия геометрии масс, обсудим простейшие вещи, связанные с барицентрическим координатами, подготовимся к основной части спецкурса.

Открытая неделя проводится 22-27 июля.

➤ «Интенсив по барицентрам» 2 часть

На самом интенсиве мы погрузимся в пучину барицентров, решим множество задач уровня сложнейших математических состязаний.

Преподаватель — Бахарев Федор Львович.

Интенсив проводится 28 июля - 4 августа.

➤ «Дистанционные графы»

Преподаватель — Дидин Максим Александрович.

Погружение в теорию графов для любителей комбинаторики. Обсудим число независимости графа и его хроматическое число, научимся доказывать известные теоремы про графы и попробуем решить открытые вопросы.

Занятия проводятся 17-23 августа.

Запись на спецкурсы откроется совсем скоро! Не пропустите🔥

Думаете, всё знаете про степень точки? А вот и нет.

Тринадцатая задачная разминка — от нашего преподавателя Фёдора Львовича Бахарева. Комментарий от автора:

В этой разминке мы затронем довольно сложные и содержательные вопросы, связанные со сравнительно свежими подходами к решению трудных геометрических задач. Речь пойдёт об алгебраическом взгляде на степень точки относительно окружности, то есть о понимании степени точки как функции на плоскости. На разборе мы затронем такие важные темы, как линейность разности степеней относительно двух окружностей и лемма о соосности. Возможно, на разборе будут разобраны не только три задачи, приведённые выше, но и некоторые задачи из последних олимпиад, например, с финала ВсОШ этого года.

Разминка будет полезна всем, кто уже знает, что такое степень точки, но хочет освоить продвинутые техники её использования.

Как всегда, в комментариях приветствуются ваши решения и мысли о задачах.

Разбор задач будет проводиться Фёдором Львовичем в субботу 22 июня в 15:00 мск по ссылке https://us06web.zoom.us/j/5634707332?pwd=TUcxTlJQbmxxMGRucDJ0ejVDaVZ3UT09&omn=84130329096

Присоединяйтесь!

#мт_разминка

Придумал окружности анти-Аполлония треугольника (наверняка, не я первый). A-окружность анти-Аполлония треугольника ABC это геометрическое место точек X таких, что BX/CX=CA/BA.

Оказывается они очень похожи на окружности Аполлония.

1. Если такие окружности пересекаются, то они все три пересекаются в двух точках, симметричных относительно описанной окружности треугольника.

2. Они соосны.

3. Они перпендикулярны описанной окружности.

4. Их общая радикальная ось — прямая Эйлера треугольника.

Что еще можно про них сказать? Или про точки их пересечения? Ну и вообще это все, наверное, давно исследовано и как-то называется...

Напоминаем, что сегодня в 15:00 мск будет проходить разбор задач от Фёдора Львовича Бахарева.

Будем обсуждать тринадцатую задачную разминку, посвящённую степени точки и продвинутым техникам вокруг неё. Условия задач можно найти тут.

Ссылка для подключения

Присоединяйтесь!

Зеленый четырехугольник — квадрат. Зеленый угол равен 45 градусов. Докажите, что разность красного и синего угла тоже 45 градусов.

USA TSTST 2024, problem 4

Диагонали вписанного четырхугольника ABCD пересекаются в точке E. Касательные в точке A к (AED) и в точке C к (BCE) пересекаются в точке P. Касательные в точке D к (AED) и в точке B к (BCE) пересекаются в точке Q. Докажите, что точки P и Q равноудалены от центра (ABCD).

30 способов охарактеризовать симедиану от Луиса Гонсалеса!

А вот такое интересное "доказательство" теоремы Монжа (о трех колпаках), говорят принадлежит Акопяну

Заметим, что точка пересечения общих внешних касательных к двум окружностям обладает тем свойством, что любая прямая, проходящая через эту точку составляет равный угол с этими двумя окружностями. При этом верно и обратное утверждение. Следовательно, прямая, проходящая через два центра гомотетии, составляет равные углы со всеми тремя окружностями, а значит проходит и через третий центр гомотетии.