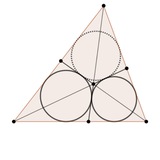
Продолжаем субботнюю традицию! Еще одна классная точка, которая мне очень нравится и довольно часто возникает в задачах. Она тесно связана с предыдущими, что дает о ней много дополнительной информации!
✍43🔥23❤10👍3🥰3🐳3🦄3❤🔥1👎1👻1
Forwarded from Математические кружки | «МТ кружки»
Так ли просты круги, как кажется?
Юбилейная десятая задачная разминка — от нашего преподавателя Александра Викторовича Смирнова. Его комментарий:
Как обычно, в комментариях приветствуются ваши решения и мысли о задачах.
Разбор задач будет проводиться Александром Викторовичем в субботу 1 июня в 17:00 мск по ссылке https://us06web.zoom.us/j/84684076104?pwd=O6FzBMTsUmjCwfRQDoGD6CAaybAkY1.1
Meeting ID: 846 8407 6104
Passcode: 323214
Присоединяйтесь!
#мт_разминка
Юбилейная десятая задачная разминка — от нашего преподавателя Александра Викторовича Смирнова. Его комментарий:
Сегодня задачи по геометрии, но не простой, а комбинаторной! От классической планиметрии они отличаются формулировками, приближенными к реальной жизни. Ведь каждый из нас хоть раз сталкивался со схожими вопросами, когда собирал портфель в школу
или, например, расставлял мебель в комнате.
Обычно для решения таких задач не нужно каких-то специальных знаний, достаточно сообразительности.
Однако на разборе мы обсудим некоторые общие приёмы, помогающие при решении. И даже замахнёмся на задачу 4б, для решения которой придётся придумать хитроумную теорию!
Как обычно, в комментариях приветствуются ваши решения и мысли о задачах.
Разбор задач будет проводиться Александром Викторовичем в субботу 1 июня в 17:00 мск по ссылке https://us06web.zoom.us/j/84684076104?pwd=O6FzBMTsUmjCwfRQDoGD6CAaybAkY1.1
Meeting ID: 846 8407 6104
Passcode: 323214
Присоединяйтесь!
#мт_разминка
✍10👍9❤4🥰4🤡4😱1🌚1
В задаче 4, кстати, действительно очень крутая история ее создания и решения! А решение и аппарат для этого решения, насколько я знаю, придумал абсолютно легендарный геометр Виктор Абрамович Залгаллер.
Есть, кстати, несколько записанных диалогов с Залгаллером, если вы интересуетесь математикой и ее историей, это очень интересно.
https://youtu.be/1ZJBraHCpbA?si=66CrFaV_uWSA8rzh
Есть, кстати, несколько записанных диалогов с Залгаллером, если вы интересуетесь математикой и ее историей, это очень интересно.
https://youtu.be/1ZJBraHCpbA?si=66CrFaV_uWSA8rzh
YouTube
В.А. Залгаллер рассказывает 2
Запись сделана в Реховоте (Израиль) 30.10.2009
🔥15❤3🥰3
Всем привет! Немножечко спама вам в ленту! Опять неумолимо приближается лето и ваши любимые преподаватели уже чувствуют, что еще чуть-чуть и можно будет, наконец, вздохнуть с облегчением, никого не учить и отдохнуть. А что же делать вам? Как провести лето с пользой?
Как и год назад для вас есть куча разных лагерей, интенсивов, вебинаров, курсов и пр., на которых вы сможете отвлечь себя от ненавистного летнего отдыха. Одно расстраивает — перерывы между летними школами, которые просто нечем заполнить. Да и в летних школах с лагерями, порой, остается еще куча свободного времени, которое просто некуда засунуть. Ну действительно, не идти же гулять и дышать свежим воздухом...
Короче, как и год назад Давид Юрьевич Бродский организует свои супер-мега-пупер-классные курсы по геометрии. В этом году есть возможность учиться на трех уровнях сложности — можно подобрать себе наиболее комфортный.
Что полезно знать
► Продолжительность — 3 месяца, то есть можно заниматься все лето
► Раз в неделю выкладывается 1-2 лекции с теоретическим материалом
► Раз в неделю предлагается серия задач, которая проверяется преподавателями через таксу Дусю
► Раз в неделю онлайн разбор с Давидом Юрьевичем, где вы ему можете задать самые неожиданные вопросы
► На каждой неделе будут челлендж-задачки для тех, кто решил все основные
► Все материалы курса доступны до конца курса и даже немного дольше
► Для тех, кто все-таки отвлекается на всякие там лагеря и летние олимпиады, типа IMO, предусмотрен сдвиг дедлайнов и сроков доступа к материалам
Короче, заниматься можно в довольно лайтовом режиме и позволять себе паузы, и при этом круто прокачать себе геометрию всего за одно лето.
За подробностями ныряйте по ссылке
Ну и картинка к посту нужна. Вот вам одна из самых красивых задач Давида Юрьевича — задача через которую я вообще узнал о существовании такого человека.
Оказывается, ортоцентр треугольника с вершинами в серединах биссектрис лежит на прямой Эйлера исходного.
Как и год назад для вас есть куча разных лагерей, интенсивов, вебинаров, курсов и пр., на которых вы сможете отвлечь себя от ненавистного летнего отдыха. Одно расстраивает — перерывы между летними школами, которые просто нечем заполнить. Да и в летних школах с лагерями, порой, остается еще куча свободного времени, которое просто некуда засунуть. Ну действительно, не идти же гулять и дышать свежим воздухом...
Короче, как и год назад Давид Юрьевич Бродский организует свои супер-мега-пупер-классные курсы по геометрии. В этом году есть возможность учиться на трех уровнях сложности — можно подобрать себе наиболее комфортный.
Что полезно знать
► Продолжительность — 3 месяца, то есть можно заниматься все лето
► Раз в неделю выкладывается 1-2 лекции с теоретическим материалом
► Раз в неделю предлагается серия задач, которая проверяется преподавателями через таксу Дусю
► Раз в неделю онлайн разбор с Давидом Юрьевичем, где вы ему можете задать самые неожиданные вопросы
► На каждой неделе будут челлендж-задачки для тех, кто решил все основные
► Все материалы курса доступны до конца курса и даже немного дольше
► Для тех, кто все-таки отвлекается на всякие там лагеря и летние олимпиады, типа IMO, предусмотрен сдвиг дедлайнов и сроков доступа к материалам
Короче, заниматься можно в довольно лайтовом режиме и позволять себе паузы, и при этом круто прокачать себе геометрию всего за одно лето.
За подробностями ныряйте по ссылке
Ну и картинка к посту нужна. Вот вам одна из самых красивых задач Давида Юрьевича — задача через которую я вообще узнал о существовании такого человека.
Оказывается, ортоцентр треугольника с вершинами в серединах биссектрис лежит на прямой Эйлера исходного.
❤25✍6🤡4🥰3😁3👍2👏2🦄2💊2
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Пока самая красивая задача этого сезона. LMAO 2024 P3. Дан равносторонний оранжевый треугольник и точка P на его вписанной окружности. Точку P отразили относительно сторон оранжевого треугольника и получили красный треугольник. Далее отразили точку P относительно сторон красного треугольника и получили черный треугольник. Докажите, что описанная окружность черного треугольника касается вписанной и описанной оранжевого.
🔥57❤7🤡3✍2👎2👍1🥰1
Задача от Василия Мокина! Предлагалась на зимних сборах в сезоне 2022/2023.
Даны две зеленые окружности одна внутри другой. Две красные окружности с красными центрами и две синие окружности с синими центрами касаются одной зеленой внутренним и одной зеленой внешним образом. Четырехугольник с вершинами в красных и синих центрах - трапеция. Тогда одна из диагоналей четырехугольника, образованного парами внешних касательных к красным и к синим окружностям перпендикулярна основанию этой трапеции.
Даны две зеленые окружности одна внутри другой. Две красные окружности с красными центрами и две синие окружности с синими центрами касаются одной зеленой внутренним и одной зеленой внешним образом. Четырехугольник с вершинами в красных и синих центрах - трапеция. Тогда одна из диагоналей четырехугольника, образованного парами внешних касательных к красным и к синим окружностям перпендикулярна основанию этой трапеции.
💊58❤14🔥8✍5🤯4🤮3👍1
This media is not supported in your browser
VIEW IN TELEGRAM
для тех, кто соскучился по простым и добрым утверждениям...
думаю, что многие не задумывались о внешнем аналоге леммы Архимеда, а он есть
думаю, что многие не задумывались о внешнем аналоге леммы Архимеда, а он есть
🥰71❤🔥15❤6👍3✍2🔥2🐳2
This media is not supported in your browser
VIEW IN TELEGRAM
Шесть красных точек делят стороны треугольника в одинаковом отношении. Через них проведены две окружности (точки разбиты через одну). Оказывается, радикальная ось этих окружностей не зависит от положения красных точек и определяется самим треугольником.
🔥36❤10😭4✍3🤯2
В чате периодически пишут, что барицентрические координаты не дружат с окружностями. Не знаю, откуда взялся этот миф, если честно. Есть огромное количество задач про окружности, которые прекрасно решаются в барицентрических координатах. Вот, например, задача с майских сборов, которую я недавно выкладывал. Не поленился — написал решение.
Если вы хотите разобраться, как считать такие задачи в барицентрических координатах, то приглашаю вас на спецкурс, о котором я объявлю уже очень-очень скоро. Пока отбираю наиболее показательные задачи для разбора и решения и придумывают упражнения, которые позволят участникам накопить необходимый багаж формул.
Заменяют ли барицентрические координаты геометрические методы? Нет, не заменяют, но иногда очень хорошо дополняют и позволяют понять некоторые геометрические сюжеты глубже. Например, можно совсем в другом ключе взглянуть на лемму о соосных окружностях...
Если вы хотите разобраться, как считать такие задачи в барицентрических координатах, то приглашаю вас на спецкурс, о котором я объявлю уже очень-очень скоро. Пока отбираю наиболее показательные задачи для разбора и решения и придумывают упражнения, которые позволят участникам накопить необходимый багаж формул.
Заменяют ли барицентрические координаты геометрические методы? Нет, не заменяют, но иногда очень хорошо дополняют и позволяют понять некоторые геометрические сюжеты глубже. Например, можно совсем в другом ключе взглянуть на лемму о соосных окружностях...
👍31❤6👏6✍1
Forwarded from Авва
Прочитал про теорему Дена о разрезании: если прямоугольник можно разрезать на квадраты, то отношение его сторон рационально. Интуитивно это кажется логичным, но доказать не так уж и просто. Обратное утверждение тривиально: если отношение сторон рационально и скажем равно p/q, то увеличив масштаб в q раз, получим прямоугольник с целыми сторонами, который можно разрезать на квадраты 1x1.
Линейная алгебра помогает построить простые и красивые доказательства:
Отношение длин сторон прямоугольника W,H иррационально - это то же, что "W,H линейно независимы как векторы в пространстве R над Q". Это в свою очередь значит, что существует Q-линейная функция f:R->R, так, что f(W) и f(H) - любые удобные нам значения.
Для любой Q-линейной функции f определим f-площадь прямоугольника со сторонами A,B как f(A)*f(B). Тогда легко увидеть, что при разрезании прямоугольника на другие прямоугольники f-площадь целого равна сумме f-площади частей (это очевидно при разрезании одного прямоугольника на два, и к повторению этого можно свести любое разрезание, если сделать из него "сетку", продлив все внутренние линии до краев).
Как ни странно, доказательство почти закончено. f-площадь любого квадрата равна f(A)*f(A), то есть неотрицательна. Отсюда f-площадь любого прямоугольника размером W:H, разрезанного на квадраты, неотрицательна. Но если W/H не рационально, то мы можем выбрать такую f, что f(W)=1, f(H)=-1, и его f-площадь равна -1, это противоречие.
Другое доказательство с помощью линейной алгебры вместо f-площади пользуется тензорным произведением R@R. Если стороны прямоугольника w,h линейно независимы, то {w,h} можно продлить до базиса, и поэтому ясно, что в R@R линейно независимы также векторы w@w, w@h, h@w, h@h. С другой стороны, если прямоугольник разбит на квадраты, то w@h является суммой членов вида a@a (доказательство аналогично примеру с площадью). Это значит, что изоморфизм в R@R, который меняет координаты местами, одновременно переводит w@h в h@w и оставляет неизменным, т.е. w@h = h@w, а это противоречит их независимости.
Еще есть красивое доказательство с помощью гармонических функций на конечных графах (второе в этой заметке). А в древней книжке Яглома "Как разрезать квадрат?" (1968) есть элементарное доказательство через систему уравнений, связывающих длины сторон.
P.S. Вспоминается также замечательная статья "Fourteen proofs of a result about tiling a rectangle", где дается много доказательство похожего, но другого по сути утверждения: что если прямоугольник разрезан на прямоугольники и у каждого внутренного прямоугольника хотя бы одна из сторон - целое число, то и у всего прямоугольника тоже хотя бы одна из сторон целая.
Линейная алгебра помогает построить простые и красивые доказательства:
Отношение длин сторон прямоугольника W,H иррационально - это то же, что "W,H линейно независимы как векторы в пространстве R над Q". Это в свою очередь значит, что существует Q-линейная функция f:R->R, так, что f(W) и f(H) - любые удобные нам значения.
Для любой Q-линейной функции f определим f-площадь прямоугольника со сторонами A,B как f(A)*f(B). Тогда легко увидеть, что при разрезании прямоугольника на другие прямоугольники f-площадь целого равна сумме f-площади частей (это очевидно при разрезании одного прямоугольника на два, и к повторению этого можно свести любое разрезание, если сделать из него "сетку", продлив все внутренние линии до краев).
Как ни странно, доказательство почти закончено. f-площадь любого квадрата равна f(A)*f(A), то есть неотрицательна. Отсюда f-площадь любого прямоугольника размером W:H, разрезанного на квадраты, неотрицательна. Но если W/H не рационально, то мы можем выбрать такую f, что f(W)=1, f(H)=-1, и его f-площадь равна -1, это противоречие.
Другое доказательство с помощью линейной алгебры вместо f-площади пользуется тензорным произведением R@R. Если стороны прямоугольника w,h линейно независимы, то {w,h} можно продлить до базиса, и поэтому ясно, что в R@R линейно независимы также векторы w@w, w@h, h@w, h@h. С другой стороны, если прямоугольник разбит на квадраты, то w@h является суммой членов вида a@a (доказательство аналогично примеру с площадью). Это значит, что изоморфизм в R@R, который меняет координаты местами, одновременно переводит w@h в h@w и оставляет неизменным, т.е. w@h = h@w, а это противоречит их независимости.
Еще есть красивое доказательство с помощью гармонических функций на конечных графах (второе в этой заметке). А в древней книжке Яглома "Как разрезать квадрат?" (1968) есть элементарное доказательство через систему уравнений, связывающих длины сторон.
P.S. Вспоминается также замечательная статья "Fourteen proofs of a result about tiling a rectangle", где дается много доказательство похожего, но другого по сути утверждения: что если прямоугольник разрезан на прямоугольники и у каждого внутренного прямоугольника хотя бы одна из сторон - целое число, то и у всего прямоугольника тоже хотя бы одна из сторон целая.
👍22🔥14❤6🤮3
This media is not supported in your browser
VIEW IN TELEGRAM
По наводке Бори Трушина вот вам трэш-теорема. Пользуйтесь и не благодарите! Такого в школе и правда не расскажут!
😁156🤡54🤣28❤6🔥4🤔1
Forwarded from Геометрия-канал (Grigory Merzon)
доказать, что большой четырехугольник описанный
❤21👍4🔥2👎1