Добрая задача из шортлиста юниорской балканской олимпиады

PS мне почему-то кажется, что я эту задачу видел на какой-то российской олимпиаде...

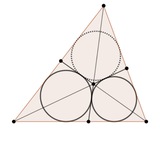
Балканская математическая олимпиада, 2024, задача 1.

Доказать, что пунктирные окружности касаются

Всем привет! Самое время для анонса! Почти ровно через две недели 14-го мая в 17:00 по московскому времени мы повторим эксперимент: на нашем канале состоится лекция Павла Витальевича Бибикова, на которой мы обсудим много интересного и нетривиального!

О неожиданных конструкциях в евклидовой геометрии: как коники, инволюции и геометрия Лобачевского помогают понимать задачи классической геометрии.

На лекции будет рассказано о неожиданной связи классической школьной геометрии и конструкциях, которые традиционно считаются весьма далекими от тех, которые знакомы и известны школьникам. Мы начнем с воспоминаний о прошедшем финале ВсОШ и обсудим решения задач 9.4 и 10.4 с помощью прямоугольных гипербол, поговорим о теореме Дезарга об инволюции и ее применении в задаче 11.4, а затем обсудим задачу, предлагавшуюся несколько лет назад участникам сборной России на Международную математическую олимпиаду, для понимания природы которой оказывается полезной геометрия Лобачевского. В ходе лекции будут также поставлены открытые вопросы и проблемы, над которыми можно думать самостоятельно.

Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения). Также будет полезно знание определений конических сечений (эллипс, гипербола, парабола).

Задача с командной олимпиады проходящего сейчас Уральского турнира.


Даны два равных правильных треугольника. Красные точки — их центры. Доказать, что линия, соединяющая центры перпендикулярна IJ.

Добрая задача с питерской олимпиады 9-го класса.

Красивая идейная первомайская задача с финала ВсОШ.

Более запутанная версия с той же олимпиады, но 11-го класса.

Всем привет! Когда-то давно я делал доклад на одном семинаре и рассказывал про задачи, которые решаются с помощью теоремы о бабочке и о некоторых обобщениях. К сожалению, семинар этот перестал существовать, а вместе с ним и его ютуб канал. Но мне удалось добыть запись и теперь она выложена на нашем канале. Мне кажется, она удачно дополняет лекцию про погружение в теорему о бабочке.

https://youtu.be/LBxLz374Q6A?si=4rGWakkNbfp33YGh

В 1965-м году задача предлагалась на Московской олимпиаде в 10-м классе, а в 1968-м году — на Ленинградской олимпиаде, но уже в 9-м классе...

Не самая хитрая и симпатичная задача с финала ВсОШ.

Требуется доказать, что в указанной конструкции три точки лежат на одной пунктирной прямой (все остальное дано).