Forwarded from fp math (Fedor Petrov)
Ездил на Всероссийскую олимпиаду. Там дети массово повадились решать геометрию с помощью ТДИ. Я раньше думал, когда изредка встречал в работах эту аббревиатуру, что школьник мне так снисходительно говорит "ты дебил идиот". А это теорема Дезарга об инволюции. Я несколько раз узнавал, в чём она состоит, и сразу забывал, а сейчас решил, наконец, разобраться.
Интересно, что хотя Жерар Дезарг жил в XVII веке, теорема стала популярной только сейчас: когда я был школьником, никто ничего не слышал про такое.
Теорема Дезарга об инволюции говорит следующее.
Пусть L - некоторое двумерное пространство в трёхмерном пространстве квадратных трёхчленов. Для точки x на прямой есть один трёхчлен из L, обнуляющийся в x. Второй корень этого трёхчлена назовем f(x). Тогда f(x) - инволюция прямой, а теорема в том, что она проективная (= дробно-линейная) .
Доказательство: в L есть линейная функция, не умаляя общности, это функция x, тогда произведение корней у всех ребят из L одинаковое по теореме Виета, поэтому f(x)=const/x.
В геометрии это обычно применяют в таком разрезе. Пусть есть 4 точки на плоскости и прямая p. Рассмотрим пучок коник, проходящих через эти 4 точки. Множество их уравнений это двумерное пространство многочленов от двух букв степени (не выше) 2. Сужая на p, получаем то самое пространство L многочленов уже от одной буквы. То есть инволюция, переставляющая точки пересечения коник этого пучка с p, проективная.
В качестве коник обычно выступают пары прямых (их есть три штуки: уже выходит нетривиальное утверждение) и (опционально) окружность.
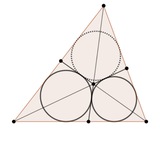
Полезно также проективно двойственное утверждение: если дана точка P и рассматриваются коники, касающиеся 4 данных прямых, то есть проективная инволюция, меняющая местами касательные из P к таким коникам. Например, пусть ABCD - описанный четырёхугольник, тогда есть инволюция, меняющая местами пары прямых PA, PC; PB, PD; касательные из P к его вписанной окружности.
Интересно, что хотя Жерар Дезарг жил в XVII веке, теорема стала популярной только сейчас: когда я был школьником, никто ничего не слышал про такое.
Теорема Дезарга об инволюции говорит следующее.
Пусть L - некоторое двумерное пространство в трёхмерном пространстве квадратных трёхчленов. Для точки x на прямой есть один трёхчлен из L, обнуляющийся в x. Второй корень этого трёхчлена назовем f(x). Тогда f(x) - инволюция прямой, а теорема в том, что она проективная (= дробно-линейная) .
Доказательство: в L есть линейная функция, не умаляя общности, это функция x, тогда произведение корней у всех ребят из L одинаковое по теореме Виета, поэтому f(x)=const/x.
В геометрии это обычно применяют в таком разрезе. Пусть есть 4 точки на плоскости и прямая p. Рассмотрим пучок коник, проходящих через эти 4 точки. Множество их уравнений это двумерное пространство многочленов от двух букв степени (не выше) 2. Сужая на p, получаем то самое пространство L многочленов уже от одной буквы. То есть инволюция, переставляющая точки пересечения коник этого пучка с p, проективная.
В качестве коник обычно выступают пары прямых (их есть три штуки: уже выходит нетривиальное утверждение) и (опционально) окружность.
Полезно также проективно двойственное утверждение: если дана точка P и рассматриваются коники, касающиеся 4 данных прямых, то есть проективная инволюция, меняющая местами касательные из P к таким коникам. Например, пусть ABCD - описанный четырёхугольник, тогда есть инволюция, меняющая местами пары прямых PA, PC; PB, PD; касательные из P к его вписанной окружности.
У нас на канале ТДИ обсуждалась в видео про теорему о бабочке. Если вы знаете про двойные отношения и инверсию, то поймете и ТДИ, и как она используется для доказательства теоремы о бабочке.
https://youtu.be/NIx_QnGemtc?si=x7ismx-1UAwC0akm&t=3964
https://youtu.be/NIx_QnGemtc?si=x7ismx-1UAwC0akm&t=3964
YouTube
#27. Погружение в теорему о бабочке
В этом видео мы обсуждаем теорему о бабочке, ее историю, некоторые доказательства от совсем элементарных до крайне глубоких, а затем рассказываем о некоторых обобщениях и схожих результатах.
00:00 intro + варианты формулировки
00:03:17 немного истории про…
00:00 intro + варианты формулировки
00:03:17 немного истории про…
Несколько замечательных свойств одной замечательной точки, у которой пока нет замечательного названия...
Forwarded from Олимпиадная математика ВсОШ | Дабромат
☀️🕶️ Летние курсы по геометрии от Дабромат
А мы не сидим на месте! Для тех, кто хочет максимально прокачаться в геоме за лето, мы запускаем «Трижды совершенный курс по геометрии», состоящий из трех ступеней.
Все курсы ведет тренер сборной Москвы Бродский Давид.
➤ «I СТУПЕНЬ»
Для кого подойдет?
Программа рассчитана на переходящих в девятый класс, а также на сильных восьмиклассников. Мы ожидаем от слушателей знание школьной программы по геометрии за 7-8 класс вплоть до понятия площадей и подобия.
По итогам прохождения курса ученик сможет уверенно решать задачи по геометрии уровня ММО, Турнира городов и регионального этапа ВсОШ по математике.
Курс подойдет и тем людям, которые знают заявленные в программе темы, но испытывают трудности в решении задач.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа — трудных дополнительных задач для тех, кому жизнь кажется слишком простой
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
— Экзамен по окончании курса
➤ «2 СТУПЕНЬ»
Для кого подойдет?
Программа рассчитана на людей, которые хорошо знают первую ступень. Для поступления надо подтвердить свой уровень знаний входным тестированием/первым дипломом ММО и аналогичных по сложности олимпиад/проходом на финал ВсОШ по математике. В случае провала вступительного испытания ученик будет зачислен на ступень ниже.
По итогам прохождения курса вы узнаете большую часть стандартных профессиональных геометрических конструкций, научитесь решать задачи уровня финала ВсОШ по математике.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа — трудных дополнительных задач для тех, кому жизнь кажется слишком простой
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
— Экзамен по окончании курса
➤ «3 СТУПЕНЬ»
В первую очередь курс рассчитан на учеников регулярного годового курса «Современная геометрия». Мы верим, что все, кому подходит этот курс, сами смогут определить это, прочитав программу. Ступень посвящена сложным геометрическим конструкциям и техникам, помогающим справляться с крайне трудными задачами. Для зачисления на курс необходимо заполнить анкету. В случае, если мы решим, что ваш опыт недостаточен для участия, вы будете переведены на ступень ниже.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа в неделю: трудные задачи для тех, кому обычные задачи кажутся слишком простыми
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
Как обычно, мы будем НЕ рады членам сборной Москвы десятого класса, которые и так занимаются у нас в кружке в Хамовниках: извольте регулярно посещать кружок в течение года, а не уповать на наши летние активности. Участие членов сборной Москвы допустимо лишь в том случае, если вы сможете обосновать необходимость этого курса для вас главному преподавателю Бродскому Давиду.
Ну а совсем скоро мы объявим о летних спецкурсах на разные темы! От алгебры и круговых многочленов до введения в топологию для старшеклассников…
Подписывайтесь на наш канал, чтобы не пропустить новые анонсы!
А мы не сидим на месте! Для тех, кто хочет максимально прокачаться в геоме за лето, мы запускаем «Трижды совершенный курс по геометрии», состоящий из трех ступеней.
Все курсы ведет тренер сборной Москвы Бродский Давид.
➤ «I СТУПЕНЬ»
Для кого подойдет?
Программа рассчитана на переходящих в девятый класс, а также на сильных восьмиклассников. Мы ожидаем от слушателей знание школьной программы по геометрии за 7-8 класс вплоть до понятия площадей и подобия.
По итогам прохождения курса ученик сможет уверенно решать задачи по геометрии уровня ММО, Турнира городов и регионального этапа ВсОШ по математике.
Курс подойдет и тем людям, которые знают заявленные в программе темы, но испытывают трудности в решении задач.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа — трудных дополнительных задач для тех, кому жизнь кажется слишком простой
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
— Экзамен по окончании курса
➤ «2 СТУПЕНЬ»
Для кого подойдет?
Программа рассчитана на людей, которые хорошо знают первую ступень. Для поступления надо подтвердить свой уровень знаний входным тестированием/первым дипломом ММО и аналогичных по сложности олимпиад/проходом на финал ВсОШ по математике. В случае провала вступительного испытания ученик будет зачислен на ступень ниже.
По итогам прохождения курса вы узнаете большую часть стандартных профессиональных геометрических конструкций, научитесь решать задачи уровня финала ВсОШ по математике.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа — трудных дополнительных задач для тех, кому жизнь кажется слишком простой
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
— Экзамен по окончании курса
➤ «3 СТУПЕНЬ»
В первую очередь курс рассчитан на учеников регулярного годового курса «Современная геометрия». Мы верим, что все, кому подходит этот курс, сами смогут определить это, прочитав программу. Ступень посвящена сложным геометрическим конструкциям и техникам, помогающим справляться с крайне трудными задачами. Для зачисления на курс необходимо заполнить анкету. В случае, если мы решим, что ваш опыт недостаточен для участия, вы будете переведены на ступень ниже.
Как все будет устроено?
— 1-2 лекции в записи каждую неделю
— 1 серия задач на неделю, содержащая как задачи на новые темы, так и задачи на повторение уже пройденного
— 1-3 челленджа в неделю: трудные задачи для тех, кому обычные задачи кажутся слишком простыми
— 1 разбор в прямом эфире с возможностью задать вопросы каждую неделю
Как обычно, мы будем НЕ рады членам сборной Москвы десятого класса, которые и так занимаются у нас в кружке в Хамовниках: извольте регулярно посещать кружок в течение года, а не уповать на наши летние активности. Участие членов сборной Москвы допустимо лишь в том случае, если вы сможете обосновать необходимость этого курса для вас главному преподавателю Бродскому Давиду.
Ну а совсем скоро мы объявим о летних спецкурсах на разные темы! От алгебры и круговых многочленов до введения в топологию для старшеклассников…
Подписывайтесь на наш канал, чтобы не пропустить новые анонсы!
dabromat.ru
Олимпиадная математика Дабромат
Курсы по олимпиадной математике
Forwarded from NeuroGeometry (Пучков Пётр)
Задача 49:
Автор - Пучков Пётр, GeoGen
Ещё одна задача про точку без названия из Олимпиадной геометрии
В треугольнике ABC проведена высота AD, а Ш - точка Шалтая для вершины A. Прямая, проходящая через why-точку и точку D, вторично пересекает описанную окружность треугольника AШD в точке E. Докажите, что середина M отрезка между why-точкой и точкой A равноудалена от E и Ш.
Автор - Пучков Пётр, GeoGen
Ещё одна задача про точку без названия из Олимпиадной геометрии
В треугольнике ABC проведена высота AD, а Ш - точка Шалтая для вершины A. Прямая, проходящая через why-точку и точку D, вторично пересекает описанную окружность треугольника AШD в точке E. Докажите, что середина M отрезка между why-точкой и точкой A равноудалена от E и Ш.