This media is not supported in your browser
VIEW IN TELEGRAM
На сториз бустов не хватает, так что пусть будет по-старинке. Тренировки тут
Тренировка полезна тем, кто хочет узнать базовые свойства изогонального сопряжения и увидеть, как это работает в задачах. Материал не сложный, но крайне полезный.
Тренировка полезна тем, кто хочет узнать базовые свойства изогонального сопряжения и увидеть, как это работает в задачах. Материал не сложный, но крайне полезный.
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Вроде доступная задача. O и H являются центром описанной окружности и ортоцентром треугольника соответственно.
This media is not supported in your browser
VIEW IN TELEGRAM
Еще одна добрая задача про два квадрата.
This media is not supported in your browser
VIEW IN TELEGRAM
Добрая задача про параллелограмм
This media is not supported in your browser
VIEW IN TELEGRAM
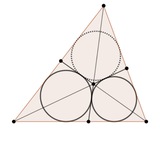
Теорема Kariya