Две очень похожих задачи

VIKKi - Ringel Circles Problem - YouTube
https://www.youtube.com/watch?v=s-3OwgwT7qw

Точка Эйлера-Понселе для парабол с параллельными осями. Предлагается найти еще свойство этой точки, которое верно для окружностей и для парабол.

Было такое популярное сообщество Проецируй... завтра на разборе Тренировок по геометрии будем разбирать задачу с эмблемы... там, кстати, то, что высота не важно...

Стрим по проективному движению точек

В 19 : 00 Давид Бродский проведет стрим, посвященный проективному движению точек в геометрии. Стрим рассчитан на учеников 10-11 класса, которые готовятся к финалу ВсОШ по математике, но может быть интересен и более младшим школьникам, серьезно увлекающимся геометрией, а также преподавателям.

Движение точек — мощный метод решения геометрических задач, который в последние годы стал крайне популярен среди школьников и преподавателей за счет своей кажущейся простоты и невероятной силы — многие труднейшие задачи финала ВсОШ и международной олимпиады развинчиваются динамическими методами на раз-два. Однако в подавляющем большинстве случаев школьники неправильно понимают концепции теории движения точек, из-за чего пишут на олимпиадах решения, содержащие серьезные ошибки.

На стриме мы поговорим об одном из самых простых видов движения — о проективном. Мы разберем несколько задач, которые в свое время считались крайне трудными, но в одну строчку решаются при помощи указанного метода. Более того, мы очень подробно поговорим о том, как нужно оформлять подобные решения на олимпиадах ,чтобы не терять баллы на оформлении.

Если вы планируете участвовать в стриме, то убедитесь, что вы знаете что такое проективная прямая, проективная плоскость и двойные отношения — без этого на стриме булет тяжке (достаточно вникнунь в определения на википедии).

Более подробно про проективный движ мржно прочитать в проекте ЛКТГ Давида Бродского.

https://youtube.com/live/7JhJzZumL34?feature=share

Задачки к стриму можно посмотреть в комментариях к посту.

Очень красивая задача из Demo варианта олимпиады JB. Задача ранее предлагалась на израиьском TST в 2021 году.

Точка H — ортоцентр треугольника ABC. Доказать, что одна из общих внешних касательных к вписанным в треугольники ABH и ACH окружностям параллельна стороне BC.

Забавно, что рефлексируя над этой задачей я придумал вариацию, которая практически в точности повторяет задачу с израильской национальной олимпиады этого года 2024.

напомнили тут в чате, одну из самых сложных задач на канале... почти 4 года прошло)

Новая задача! Синие отрезки равны, доказать, что красные углы равны.

Я тут внезапно осознал, что на следующей неделе начинается весна. А значит заканчивается заочный этап олимпиады Шарыгина (кстати, в этом году на его решение дали на один день больше, чем в прошлом). В прошлом году, кажется, довольно позитивно прошел аттракцион с решением задач в прямом эфире... В этом году я опять не смотрел на задачи заочного тура, чтобы иметь возможность повторить опыт. Такой стрим можно было бы устроить в следующее воскресенье с 17-00 до 21-00 по московскому времени. Если вам кажется эта идея привлекательной, поставьте какую-нибудь позитивную реакцию.

"Задачка відеороликом"

Секрет незайманої білої області з попереднього шортса полягає в тому, що при обертанні чотирикутника Понселе (інколи його ще називають біцентричним) синє коло завжди буде дотикатися, до сталого кола на площині.

Сложной геометрии для олимпиады JB, которая прошла сегодня, ни подобрать, ни придумать не удалось... зато в старшей лиге обе задачи были про равносторонние многоугольники.

1. В пятиугольнике ABCDE все стороны имеют единичную длину, а углы B и D дополняют друг друга до развернутого. Найдите расстояние от вершины C до точки пересечения диагоналей AD и BE.

2. Даны две не обязательно концентрические окружности, одна расположена внутри другой (тем самым они ограничивают кольцо). Выпуклый многоугольник с равными сторонами таков, что каждая из сторон пересекат обе окружности в двух точках. Докажите, что отрезки высекаемые кольцом на периметре мнгоугольника можно разбить на две группы с равными суммами.

На Тренировках по геометрии на следующей неделе учимся леммам о Воробьях. Хорошая милая тема, польза от которой может быть на любом уровне сложности. Задачи и лекция уже доступны

https://dabromat.ru/trengeom

Не сложная и красивая задача.

Всем привет! Согласовал с начальством!

Давайте проведем в воскресенье 3-го марта с 16:00 до 20:00 (по московскому времени) стрим с решением задач заочного тура олимпиады Шарыгина этого года. Присоединяйтесь в любое время, буду рад!

UPD. Говорят, отправка решений продлена до 4-го марта. Так что стрима в воскресенье не будет. Отдыхаем 😴

Может тогда в понедельник с 17 до 21? или во вторник? Можно же уже будет?

Возвращаясь к хайповой теме. Как оценить сложность геометрической задачи. И какая задача самая сложная...

PS. Послушал тут случайно небольшой доклад на тему... Говорят, следующие на очереди неравенства...

PPS. Что там, кстати, за самая сложная геометрическая задача на 247 шагов?

Грустный сегодня день...

Вышло очередное обновление геометрии на Сириус курсах. От девятого класса отделился кусок в 10-11 класс и теперь будет жить и развиваться самостоятельной жизнью. В 9-м классе мы немного переделали модуль про лемму о трезубце, добавили материалы про точку Шалтая и точку Болтая, ну и про симедиану.

На этом, похоже, мое сотрудничество с курсами закончилось: все что я знал, я рассказал. Хотелось бы надеяться, что временно, но ведь нет ничего более постоянного, чем временное...

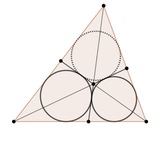
Romanian Masters of Mathematics, 2024, Problem 5.

Жирные красные точки не зависят от положения верхней вершины треугольника.