Forwarded from Олимпиадная математика ВсОШ | Дабромат
🔊 Эту неделю Тренировок по геометрии мы посвятим подготовке к Московской математической олимпиаде и весеннему сложному туру Турнира городов.
Занятие проведет создатель паблика «Олимпиадная геометрия» Бахарев Федор Львович.
А пока прекрасная задача с ММО от великого Андрея Кушнира:
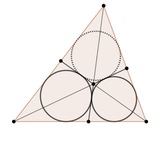
Два треугольника пересекаются по шестиугольнику, который отсекает от них 6 маленьких треугольников. Радиусы вписанных окружностей этих шести треугольников равны. Докажите, что радиусы вписанных окружностей двух исходных треугольников также равны.
Занятие проведет создатель паблика «Олимпиадная геометрия» Бахарев Федор Львович.
А пока прекрасная задача с ММО от великого Андрея Кушнира:
Два треугольника пересекаются по шестиугольнику, который отсекает от них 6 маленьких треугольников. Радиусы вписанных окружностей этих шести треугольников равны. Докажите, что радиусы вписанных окружностей двух исходных треугольников также равны.
Пока организаторы олимпиады Шарыгина думают, на какое бы еще число сдвинуть дедлайн заочного тура, я им сообщу, что следующий свободный четырехчасовой слот у меня только в пятницу.
А пока вот вам шедевр из шортлиста RMM прошлого года.
Дан треугольник ABC и точка P. Красные точки — центры окружностей (ABP), (BCP), (CPA). Доказать, что точки P и Q изогонально сопряжены относительно ABC.
А пока вот вам шедевр из шортлиста RMM прошлого года.
Дан треугольник ABC и точка P. Красные точки — центры окружностей (ABP), (BCP), (CPA). Доказать, что точки P и Q изогонально сопряжены относительно ABC.
This media is not supported in your browser
VIEW IN TELEGRAM
На этой неделе не было еще короткого видосика. Вот он! Со свеженькими материалами с Сириус.Курсов
Finally... Завтра 8-го марта с 17-00 до 21-00 по московскому времени я буду решать задачи заочного тура олимпиады Шарыгина.
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
YouTube
#9str. Прорешиваем заочный тур олимпиады Шарыгина 2024
В этом стриме мы будем прорешивать задачи заочного тура олимпиады Шарыгина, который завершился на днях. Я буду делать это без предварительной подготовки в режиме онлайн.
Аааа... я дорешал 11-ую задачу. У меня супер классное решение после инверсии. Напишу чуть позже.
Ну и в 20-ой я написал неправильную ключевую формулу, с если б написал правильно, то все, кажется, сошлось бы)
Какие вам задачи-то понравились?
Ну и в 20-ой я написал неправильную ключевую формулу, с если б написал правильно, то все, кажется, сошлось бы)
Какие вам задачи-то понравились?
Forwarded from Геометрия-канал (Grigory Merzon)
На боковых сторонах AB и BC равнобедренного остроугольного треугольника берут такие точки M и K, что угол MEA равен углу ABC (E — пересечение CM и AK). Доказать, что середины всевозможных отрезков MK лежат на одной прямой.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
Задача с питерской городской олимпиады 9.3. Автор Церен Французов.
Вызвала неожиданные трудности у девятиклассников.Видимо, нестандартностью формулировки и ощущением, что надо делать какие-то геометрические построения.
Треугольник ABC вписан в окружность. Из точек B и C одновременно выползают два муравья. Они ползут по дуге BC навстречу друг другу так, что произведение расстояний от них до точки A остается неизменным. Докажите, что во время их движения (до момента встречи) прямая, проходящая через муравьёв, касается некоторой фиксированной окружности.
Вызвала неожиданные трудности у девятиклассников.
Треугольник ABC вписан в окружность. Из точек B и C одновременно выползают два муравья. Они ползут по дуге BC навстречу друг другу так, что произведение расстояний от них до точки A остается неизменным. Докажите, что во время их движения (до момента встречи) прямая, проходящая через муравьёв, касается некоторой фиксированной окружности.
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2024/2024_zaoch_rus_sol.pdf
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
Forwarded from Geometry Weekly
#42 (Кавказская математическая олимпиада, 2024)
Дан треугольник ABC. На отрезке АС выбирается произвольная точка Х. Пусть окружность, вписанная в треугольник АВХ, касается отрезков АХ и ВХ соответственно в точках К и Р, а окружность, вписанная в треугольник СВХ, касается отрезков СХ и ВХ соответственно в точках L и Q. Найдите ГМТ пересечения прямых KP и LQ
Дан треугольник ABC. На отрезке АС выбирается произвольная точка Х. Пусть окружность, вписанная в треугольник АВХ, касается отрезков АХ и ВХ соответственно в точках К и Р, а окружность, вписанная в треугольник СВХ, касается отрезков СХ и ВХ соответственно в точках L и Q. Найдите ГМТ пересечения прямых KP и LQ
Через недельку поеду почитаю еще немного лекций кипрским студентам, а вы пока можете проверить не то ли это, что вы давно искали и хотели...
Join us on March 19, 2024, at 4:00 pm CET (3:00 pm UTC) for a livestream where we’ll introduce you to the Computer Science and Artificial Intelligence program team. Don’t miss this chance to ask questions about the admission process and find out how you can apply for a JetBrains scholarship.
Meet our guests:
Alexander S. Kulikov, DSc, Head of the Laboratory of Algorithms and Complexity Theory at JetBrains Research, Lecturer at Neapolis University Pafos (Discrete Mathematics)
Pavel Mavrin, ICPC World Champion 2004, Tutor and Researcher at JetBrains, Lecturer at Neapolis University Pafos (Algorithms: Basic Toolbox)
Alexandr Avdiushenko, Ph.D. in Math Modeling, Project Manager for the JetBrains Education and Research team, Lecturer at Neapolis University Pafos
Natalia Kitaeva, Program Coordinator, JetBrains Academy
During the livestream, you will learn more about the CSAI program structure and course curriculum, discover how admission at Neapolis University Pafos and scholarship selection work, and gain firsthand insights from our faculty. We will also discuss our approach to hands-on learning and how it prepares students for real-world challenges.
Don’t forget to register for the event to receive the livestream link and get the chance to ask your questions directly to the program’s team.
Please note that the program is still in the process of accreditation.
For more details, visit the CSAI program page.
Join us on March 19, 2024, at 4:00 pm CET (3:00 pm UTC) for a livestream where we’ll introduce you to the Computer Science and Artificial Intelligence program team. Don’t miss this chance to ask questions about the admission process and find out how you can apply for a JetBrains scholarship.
Meet our guests:
Alexander S. Kulikov, DSc, Head of the Laboratory of Algorithms and Complexity Theory at JetBrains Research, Lecturer at Neapolis University Pafos (Discrete Mathematics)
Pavel Mavrin, ICPC World Champion 2004, Tutor and Researcher at JetBrains, Lecturer at Neapolis University Pafos (Algorithms: Basic Toolbox)
Alexandr Avdiushenko, Ph.D. in Math Modeling, Project Manager for the JetBrains Education and Research team, Lecturer at Neapolis University Pafos
Natalia Kitaeva, Program Coordinator, JetBrains Academy
During the livestream, you will learn more about the CSAI program structure and course curriculum, discover how admission at Neapolis University Pafos and scholarship selection work, and gain firsthand insights from our faculty. We will also discuss our approach to hands-on learning and how it prepares students for real-world challenges.
Don’t forget to register for the event to receive the livestream link and get the chance to ask your questions directly to the program’s team.
Please note that the program is still in the process of accreditation.
For more details, visit the CSAI program page.
Forwarded from Олимпиадная математика ВсОШ | Дабромат
Новая неделя — новая Тренировка по геометрии
В эту субботу в
Для кого подойдет?
Тренировка будет полезна и готовящимся к финалу олимпиады Эйлера (пройдет 25-28 марта), и старшим ребятам, чей навык видеть в задачах дополнительные построения недостаточно развит и требует прокачки.
Что будет на тренировке?
На занятии мы будем не только применять стандартные приемы в нестандартных ситуациях, например, удвоение медианы или симметрия относительно биссектрисы, но и научимся нестандартным схемам, которые иногда встречаются на олимпиадах и могут напугать участника.
Все участники тренировки получают экспертную проверку письменных решений, так что это отличная возможность получить фидбэк непосредственно от составителей!
А за анонсами будущих тренировок следите в канале.
В эту субботу в
16:00 тренер сборной Москвы по математике, Давид Бродский, проведет очередную Тренировку по геометрии, которая, в первую очередь, ориентирована на восьмиклассную геометрию без задач на окружности. Для кого подойдет?
Тренировка будет полезна и готовящимся к финалу олимпиады Эйлера (пройдет 25-28 марта), и старшим ребятам, чей навык видеть в задачах дополнительные построения недостаточно развит и требует прокачки.
Что будет на тренировке?
На занятии мы будем не только применять стандартные приемы в нестандартных ситуациях, например, удвоение медианы или симметрия относительно биссектрисы, но и научимся нестандартным схемам, которые иногда встречаются на олимпиадах и могут напугать участника.
Все участники тренировки получают экспертную проверку письменных решений, так что это отличная возможность получить фидбэк непосредственно от составителей!
А за анонсами будущих тренировок следите в канале.
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Очень странная задачка с какой-то прошлогодней олимпиады...
Forwarded from Georgiy Chelnokov
Please open Telegram to view this post
VIEW IN TELEGRAM