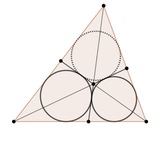
Довольно изящная задача с Тайваньской олимпиады 2024.

Точка O — центр описанной окружности треугольника ABC. Точки E и F — произвольные точки на сторонах AC и AB соответственно. Точка P такова, что PF=PB и PE=PC. Через точку P проводят две прямых: PO и перпендикуляр к FE. Доказать, что эти две прямых пересекают прямые AB и AC в четырех точках, лежащих на одной окружности.

Так-так-так... тут в чате спрашивают материалы по проективной геометрии. И даже просят какую-то конкретную книжку, про которую я даже не слышал...

Но вот, что я знаю. У Дабромата как раз открылся курс по Проективной геометрии. Ведет его в основном Давид Бродский. Кажется, это неплохой способ все узнать, понять, систематизировать, укрепить, прокачать.

Курс тут.

Ну и чтобы два раза не вставать, напоминаю, что можно про точки Шалтая потренироваться на Тренировках по геометрии со мной.

Поскидывайте в комментариях классные материалы по проективной геометрии для самообучения...

IMO Shortlist 2008, Problem G4, Proposed by Davood Vakili, Iran

В остроугольном треугольнике ABC проведены высоты BE и CF. Окружности, проходящие через точки A и F касаются прямой BC в точках P и Q. Докажите, что прямые PE и QF пересекаются на описанной окружности треугольника AEF.

PS. У меня, кстати, появилась гипотеза, откуда взялось название Humpty point. Дело в том, что их какое-то время называли HM-point, потому что они лежат на окружности с диаметром HM, где H — ортоцентр, а M — точка пересечения медиан.

#37 (Высшая проба 2024, 10.3)

В треугольнике ABC точка I — центр вписанной окружности, E и F — основания биссектрис BI и CI соответственно. Прямая AI пересекает описанную около треугольника EIF окруж- ность в точке T != I. H - ортоцентр треугольника AEF. Доказать, что ортоцентр треугольника AEF равноудален от точек T и I

Про точки Болтая скоро тоже будет Тренировка... до этого, правда, еще запланированы про задачу 255 и про гармонические четырехугольники...

красота ж

Задача 13:
Автор - GeoGen, Чуев Савва

AM - медиана в треугольнике ABC. Ib, Ic - центры вписанных окружностей треугольников ABM и ACM соответственно. Прямые BIc и CIb пересекаются в точке P. Докажите, что PM || AD, где D - точка касания вписанной окружности треугольника ABC с его стороной BC.

все точки типа 255 на одной картинке. проекции вершин на разные биссектрисы лежат на средних линиях и прямых соединяющих точки касания вписанной и вневписанных окружностей.

Они, кстати, довольно забавно располагаются по 6 штук на четырех окружностях

Мне кажется, что именно в этом канале было обсуждение вопроса о том куда все катится (в смысле в коники и кубики). Вот задачка, предложенная неким японцем под ником Tock. Ловите лемнискату Бернулли ). Если честно, то ничего подобного я ни разу не видел.

Докажите, что красные отрезки имеют одинаковую длину.

Доказать, что окружности касаются

Коротко о всяких штуках, которые меня окружают.

1. Олимпиада JB набирает обороты, в сеньоров уже зарегистрировалось больше 20 команд, в юниоров поменьше... Радует, что есть участники из разных стран и есть те, кого я лично знаю. Зарегистрироваться на олимпиаду все еще можно по ссылке. В это воскресенье будет опубликован демо-вариант.

2. На этой неделе на тренировках по геометрии мы обсуждаем задачу 255, а на следующей будем говорить про гармонические четырехугольники. Кстати, разбор на этой неделе будет по техническим причинам в воскресенье в 16:30.

3. На МТ-кружках мы вроде бы успешно почти отобрали счастливчиков, получивших стипендию для обучения. Заодно пополнили список ассистентов, чтобы на занятиях все еще можно было много и интенсивно общаться с преподавателями. Кстати, у МТ-кружков есть свой канал в телеграме, в котором скоро будет больше подписчиков, чем тут. Тренировочных олимпиад пока больше не будет, но зато будет другой полезный контент.

4. Давид Юрьевич разобрал вариант 11-го класс Высшей пробы у себя на канале. Возможно, есть смысл сбегать посмотреть, поставить лайк и все такое. Тем, кто делает контент, важно видеть обратную реакцию!

Очень крутая задача с секретом с MMO 2021(это не Московская олимпиада, а макет в стиле IMO). Предлагалась под номером 3. Картинку не рисую. Пусть ABC - неравнобедренный треугольник. Предположим, что окружность с центром на прямой BC, проходящая через A, окружность с центром на прямой AC, проходящая через B, и окружность с центром на прямой AB,проходящая через C, имеют общую радикальную ось. Докажите, что центр описанной окружности треугольника ABC лежит на этой радикальной оси.

F — точка Фейербаха

Нашел во всемирной паутине название утверждения выше. Оно оказывается называется теорема Мангейма. А пунктирные линии называются прямыми Мангейма. Они пересекаются с соответствующими средними линиями на прямой IG (соединяющей центр вписанной окружности и точку пересечения медиан).

У нас уже было одно фантастическое утверждение Мангейма на канале... думаю, это тот же крутой перец.

А вот вам на ночь абсолютно фантастическое утверждение.

(Теорема Мангейма, 1864) Даны три непересекающиеся окружности. К ним проведены шесть внутренних касательных. Оказалось, что три из них пересекаются в одной точке. Докажите, что и три другие тоже пересекаются в одной точке.

Одна из моих самых любимых задач (потому что решается очень большим количеством по существу разных способов). Самое изящное ее решение с помощью гармонических четырехугольников. Но в листик по гармоническим четырехугольникам в Тренировках я ее не включил из-за высокой сложности. В листике все-таки скорее учебные задачи, позволяющие научиться видеть базовую конструкцию в более простых задачах (пока, правда, нет участников, решивших все задачи из листика 🤔).

Задача. На картинке красная прямая касается красной окружности, синяя — синей, зеленая — зеленой. Доказать, что красная и синяя окружности пересекаются на стороне треугольника.

Кстати, на Тренировках дальнейший план такой.

Серия 11. Воробьи
Серия 12. Поворотная гомотетия
Серия 13. Точки Болтая

Мне кажется, будет хороший набор задач, чтобы погрузиться в тему. Конечно, хорошо бы при этом знать про точку Шалтая и про гармонические четырехугольники. Но если вы покупаете тренировку, то у вас есть доступ к предыдущим, так что можно посмотреть лекции и разборы!