Задача Егора Бакаева с Турнира Городов (базовый тур, 8-9 класс, осень 2024)

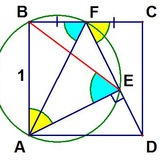
Дан описанный пятиугольник 𝐴𝐵𝐶𝐷𝐸. Центр его вписанной окружности лежит на диагонали 𝐴𝐶. Докажите, что 𝐴𝐵 + 𝐵𝐶 > 𝐶𝐷 + 𝐷𝐸 + 𝐸𝐴

Картинку мы взяли в канале Фулл и точка
А тут остальные задачи этого тура

А у 10-11 классов на Тургоре была задача Михаила Евдокимова, тоже прекрасная.

В равностороннем треугольнике ABC проведены отрезки ED и GF, так что образовались два равносторонних треугольника ADE и GFC со сторонами 1 и 100 (точки E и G лежат на стороне AC).

Отрезки EF и DG пересекаются в точке O, причём ∠EOG = 120°.

Чему равна сторона треугольника ABC?

Еще интересная теорема о замыкании.

На стороне BC треугольника выбирают точку D. B треугольники ABD и ACD вписывают окружности. Их общая внешняя касательная пересекает AD в точке K. Доказать, что длина AK не зависит от выбора точки D.

// Задача И.Ф.Шарыгина на ММО-1994 с сегодняшнего семинара. Подходит начинающим — никакие знания сверх школьной программы не требуются (но надо не полениться)

В прямоугольный треугольник вписана окружность. Через точку её касания с катетом проведён перпендикуляр к хорде, соединяющий другие две точки касния. Доказать, что этот перпендикуляр высекает на катете отрезок, равный радиусу вписанной окружности.

// Задача М.А.Волчкевича на ММО-2007 со вчерашнего семинара. Тоже не требует никаких знаний (но придумать решение не так просто). В комментариях есть обобщение

параболу y=-x² пересекают всевозможными параболами вида y=x²+ax+b, проходящими через фиксированную точку

доказать, что всевозможные общие хорды этих парабол проходят через фиксированную точку

// задача П.Кожевникова с заканчивающейся сейчас олимпиады «Ассара»; все задачи — https://tttttt.me/matheduks/31

#семинары

❗️Семинар учителей математики в МЦНМО.

Д.Г.Мухин, Д.В.Швецов. Вписанная и вневписанная окружность.

Приглашаю всех принять участие в устной олимпиаде Лицея НИУ ВШЭ по геометрии!
Олимпиада проводится для учеников 8-11 классов. Интересные задачи найдутся как для начинающих, так и для опытных геометров.
Олимпиада состоится 27 октября по адресу: ул. Солянка 14А, стр.1. Начало олимпиады в 10.00.

Для участия необходима предварительная регистрация: https://docs.google.com/forms/d/e/1FAIpQLSeYRBtcir_X2sfYnwOCrHcMahrgC2VXAAEcQC614jni048q5w/viewform?usp=sf_link
Регистрация открыта до 26 октября.

#геометрия #задача

Докажите, что пунктирная прямая проходит, через фиксированную точку.

Внутри окружности расположен а) правильный б) равносторонний многоугольник. Каждую его сторону продлевают в обе стороны до окружности — появляется по два новых отрезка. Доказать, что если новые отрезки покрасить в красный и синий цвета в естественном порядке, то сумма длин красных отрезков будет равна сумме синих.

// подниму из комментариев обобщение предыдущей задачи

Давид Бродский написал хорошие посты про инверсию. Всем рекомендую. Пост 1, Пост 2. А ну да в комментариях написали еще уровни. Но я бы сказал, что есть только еще один уровень. Он заключается в том, что инверсия является изогональным сопряжением относительно некоторого треугольника. Треугольник немного необычный правда. Две вершины у него комплексные... Но зато это позволяет расширить инверсию на комплексные точки, а еще наверное не надо доказывать, что инверсия сохраняет двойные отношения. Но к сожалению такой взгляд не очень помогает в задачах, поэтому знать необязательно)

давайте попробуем новый формат: “задачи на практическое построение”

допустим обсуждаются всевозможные окружности, касающиеся двух данных (как на рисунке) — как строить такие картинки? (например, в геогебре; или если не верите в компьютеры — циркулем и линейкой)

рассматривают всевозможные пунктирные окружности, касающиеся двух данных (внутренним образом)

доказать, что концы возникающих красных хорд лежат на одной окружности

( задача П.Кожевникова на позавчерашнем Турнире городов; все задачи: https://turgor.ru/problems/46/os-46-sl-avt.pdf )

Разминка дня №1

С этого дня команда администраторов будет делать почти каждый день разминки (простые задачи для всех, чтобы разбавить тот ужас, который постится здесь обычно. Обычные посты никуда не денутся)

#математика

Представляем вашему благосклонному вниманию новый ролик «Очень красивая задача», и к такому названию трудно что-то добавить, кроме того, что эта задача геометрическая.

Вот её условие: точка внутри равностороннего треугольника соединена тремя отрезками с его вершинами, при этом оказалось, что сумма квадратов двух отрезков равна квадрату третьего. И требуется найти угол между первыми двумя отрезками.

Решить эту задачу можно буквально одним движением, попробуйте сделать это сами! И, конечно, смотрите наше решение и не забывайте ставить лайки!

P.S. По этой ссылке можно найти ролик на других платформах.

[Поддержите нас]

Внутри правильного шестиугольника взяли другой правильный шестиугольник, после чего соединили их соответствующие вершины. Докажите, что сумма площадей красных четырехугольников равна сумме площадей синих шестиугольников. Верно ли, что сумма квадратов площадей красных равна сумме квадратов площадей синих?