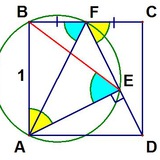
Доказательство теоремы ван Обеля. Источник.

#начинающим

Прямоугольник разрезали на семь квадратов. Площадь одного из маленьких квадратов равна 1. Найдите площадь всего прямоугольника.

Вариация теоремы о равенстве вписанных углов.

Синяя окружность дважды касается эллипса с фокусом F. Докажите равенство зеленых углов.

Как ещё увидеть, что проекция тетраэдра Серпинского вдоль линии, соединяющей середины противоположных рёбер, это квадрат?
Очень просто: нужно взять тетраэдр Серпинского, ясную, солнечную погоду и выйти на улицу.

И.И. Богданов, финал Шарыгина 2010, 8 класс, 4 задача

Листик про квадраты для начинающих геометров

Поддержим волну! Листок этой недели про квадраты для вчерашних семиклассников на основе замечательной книги А.Д. Блинкова «Геометрия стандартная и не очень». Для решения задач достаточно материала седьмого класса!

Олимпиада ЮМШ. Отборочный тур. 10 класс. Дан равносторонний треугольник ABC. Пусть M — середина отрезка BC. Точка D симметрична точке A относительно точки B, а точка
K — основание перпендикуляра, опущенного из точки C на прямую MD.
Докажите, что K лежит на вписанной окружности треугольника ABC.

Олимпиада ЮМШ. Отборочный тур. 11 класс. На кривой xy = 1 (x > 0, y > 0) даны две точки A и B. Касательные
к кривой в точках A и B пересекаются в точке F . Пусть M — середина
отрезка AB, O — начало координат. Докажите, что (MO * MF)/
(MA * MB) не зависит от точек A и B.

Раз уж пошла мода выкладывать листки выложу еще один. Листки я начал делать недавно так, что делаю это наверное не очень хорошо. Ну и ладно. Вот мой первый листок, который я выдавал. Тема листка "Нулевая окружность", то есть обсуждается радикальная ось точки(нулевой окружности) и окружности. По-моему очень красивая тема для которой не нужно знать много теории, поэтому мне захотелось сделай свой первый листик про нее)

#начинающим

На рисунке изображен паркет из равных прямоугольных треугольников. Произвольные прямоугольные треугольники для такой схемы не подойдут.

Найдите соотношение сторон в этих треугольниках.

Рисунок и задача из журнала «Квантик» №7, 2017, статья Сергея Маркелова «Жесткие паркеты»

#геом_разминка

Задача. В треугольнике две высоты не меньше сторон, на которые они опущены. Найдите
углы этого треугольника.

#красота_спасет_мир

Встречайте авторскую задачу от Ивана Андреевича 😎

Задача. Даны две касающиеся внешним образом окружности Ω₁ и Ω₂ и угол 𝛼. К Ω₁ проводится касательная 𝑙₁ в точке 𝑋, а к Ω₂ касательная 𝑙₂ в точке 𝑌 так, что ∠𝑋𝑃𝑌 = 𝛼, обе окружности лежат внутри ∠𝑋𝑃𝑌, 𝑃 лежит выше линии, соединяющей центры Ω₁ и Ω₂, где 𝑃 — точка пересечения 𝑙₁ и 𝑙₂. Докажите, что биссектриса ∠𝑋𝑃𝑌 касается фиксированной окружности.

За неподвижной картинкой заходите в комментарии и присоединяйтесь к чату канала 💪

Задача якою зі мною поділився Григорій Борисович.

Всередині арени цирку сидить тигр. По команді дресирувальника, тигр біжить у довільному напрямку до арени, та повертає два рази. Покажіть куди треба покласти шматок м'яса, щоб незалежно від напрямку, у якому біг тигр, він би на цей шматочок натрапив.

Продолжаем традицию! Листик для начинающих геометров. Немного посложнее — про правильные многоугольники.

#красота_спасет_мир #ЮМТ

Команда авторов канала сейчас на Южном математическом турнире 🙂

Мы будем держать вас в курсе событий 😉 Ожидается очень много крутых геометрий 🔥

А вот и первая — своеобразный тест на профессионала с довольно изящной формулировкой от Павла Александровича 🤗

Задача. Трапеция 𝐴𝐵𝐶𝐷 (𝐴𝐵 ‖ 𝐶𝐷) вписана в окружность Ω. Рассмотрим всевозможные окружности Γ, которые касаются отрезка 𝐶𝐷 и той дуги 𝐶𝐷 окружности Ω, что не содержит точек 𝐴 и 𝐵. Пусть Γ касается сторон некоторого угла ∠𝐴𝑃𝐵 в точках 𝐾 и 𝐿 соответственно. Докажите, что сумма 𝐴𝐾 + 𝐵𝐿 постоянна (то есть не зависит от выбора окружности Γ).

На командной олимпиаде в старшей лиге была еще одна прикольная геометрия от нашего подписчика Вовы Конышева. С ней справилась всего одна команда! 🤯

Условие и картинку к сложной задачке вы сможете найти в комментариях к посту 👇
Там же лежит неподвижная картинка к задаче от Павла Александровича 💜

Добавляйтесь в наш чат, чтобы ничего не пропустить!

Задача о которой идет речь в посте выше