Forwarded from Фулл и точка
Как мы говорили раньше, коники иногда неожиданно помогают придумать классное и короткое решение сложной задачи 💪
Так случилось на летней школе в Казани с одной из задач по мотивам проекта ЛКТГ-2015, которая была в листике Павла Александровича Кожевникова.
Участник нашего проекта и наш подписчик Иванов Госман придумал ранее неизвестное крутое решение при помощиполяр и гиперболы F (о которой см. предыдущий пост) .
Поздравляем Госмана 🥳
Публикуем условие задачи. Подумайте над ней и вы 🤔
Вдруг родится еще одна новая идея 💡
Задача. В остроугольном треугольнике 𝐴𝐵𝐶 проведены высоты 𝐴𝐻𝑎, 𝐵𝐻𝑏 и 𝐶𝐻𝑐.
Точки I и O — соответственно центры вписанной и вневписанной окружностей.
Докажите, что если I лежит на 𝐻𝑏𝐻𝑐, то прямая OI проходит через 𝐻𝑎.
Так случилось на летней школе в Казани с одной из задач по мотивам проекта ЛКТГ-2015, которая была в листике Павла Александровича Кожевникова.
Участник нашего проекта и наш подписчик Иванов Госман придумал ранее неизвестное крутое решение при помощи
Поздравляем Госмана 🥳
Публикуем условие задачи. Подумайте над ней и вы 🤔
Вдруг родится еще одна новая идея 💡
Задача. В остроугольном треугольнике 𝐴𝐵𝐶 проведены высоты 𝐴𝐻𝑎, 𝐵𝐻𝑏 и 𝐶𝐻𝑐.
Точки I и O — соответственно центры вписанной и вневписанной окружностей.
Докажите, что если I лежит на 𝐻𝑏𝐻𝑐, то прямая OI проходит через 𝐻𝑎.
в личные сообщения написали вопрос, где можно прочитать про применения выхода в комплексные числа в вещественной геометрии — мб что-нибудь посоветуете?
(имеется в виду не параметризация точек плоскости комплексными числами, а выход из R(P)² в C(P)² — e.g. радикальная ось как вещественная прямая через две комплексные точки пересечения, общие точки всех окружностей, афф. эквивалентность гипербол и окружностей [над C] и проч.)
(имеется в виду не параметризация точек плоскости комплексными числами, а выход из R(P)² в C(P)² — e.g. радикальная ось как вещественная прямая через две комплексные точки пересечения, общие точки всех окружностей, афф. эквивалентность гипербол и окружностей [над C] и проч.)
Forwarded from Фулл и точка
Еще одна задачка на скрытые коники с лаконичным условием была на одном из Южных турниров прошлых лет за авторством одного из создателей нашего канала — Ивана Кухарчука.
До решения при помощи коник догадаться очень непросто, однако оно буквально в одну строчку 😎
Ее можно решить также с помощьюдвойных отношений , но этот способ куда менее изящен. Делитесь своими решениями в комментариях 🐱
Задача. Вписанная окружность треугольника 𝐴𝐵𝐶 с центром в I касается стороны 𝐵𝐶 в точке 𝐾𝑎. Пусть L — проекция точки I на серединный перпендикуляр к отрезку 𝐴𝐾𝑎. Докажите, что LI — биссектриса угла BLC.
До решения при помощи коник догадаться очень непросто, однако оно буквально в одну строчку 😎
Ее можно решить также с помощью
Задача. Вписанная окружность треугольника 𝐴𝐵𝐶 с центром в I касается стороны 𝐵𝐶 в точке 𝐾𝑎. Пусть L — проекция точки I на серединный перпендикуляр к отрезку 𝐴𝐾𝑎. Докажите, что LI — биссектриса угла BLC.
prokopenko_-_cyclic_orthodiagonal.pdf
1.4 MB
в продолжение задачи выше — статья Д.В.Прокопенко про вписанный четырехугольник с перпендикулярными диагоналями
все знают, что сумма расстояний от точки эллипса до фокусов постоянна
оказывается, фокусы можно заменить на любые дважды касающиеся эллипса окружности — докажите, что сумма синих касательных не зависит от выбора точки эллипса (upd: между точками касания… или нужно добавить знаки)
отсюда, кстати, следует и предыдущая задача
оказывается, фокусы можно заменить на любые дважды касающиеся эллипса окружности — докажите, что сумма синих касательных не зависит от выбора точки эллипса (upd: между точками касания… или нужно добавить знаки)
отсюда, кстати, следует и предыдущая задача
Поздравляем всех с началом нового учебного года! Пусть будет интересно.
В канале стартует новая рубрика #начинающим
в ней примерно раз в неделю будут простые задачи для тех, кто только начал изучать геометрию или совсем забыл ее. Пойдем потихонечку, не торопясь обгонять семиклассников по программе.
Если для вас это слишком простые задачи, перешлите их младшим братьям, сёстрам или друзьям.
Начнем с задачи, в следующем посте. Она оформлена в виде опроса, но не в режиме викторины, то есть правильный ответ не будет виден сразу. Его мы опубликуем в комментариях через неделю перед публикацией новой задачи рубрики.
upd. Правильный ответ хорошо виден по статистике ответов. Решение в комментариях несколько раз написали. Спасибо поучаствовавшим.
В канале стартует новая рубрика #начинающим
в ней примерно раз в неделю будут простые задачи для тех, кто только начал изучать геометрию или совсем забыл ее. Пойдем потихонечку, не торопясь обгонять семиклассников по программе.
Если для вас это слишком простые задачи, перешлите их младшим братьям, сёстрам или друзьям.
Начнем с задачи, в следующем посте. Она оформлена в виде опроса, но не в режиме викторины, то есть правильный ответ не будет виден сразу. Его мы опубликуем в комментариях через неделю перед публикацией новой задачи рубрики.
upd. Правильный ответ хорошо виден по статистике ответов. Решение в комментариях несколько раз написали. Спасибо поучаствовавшим.
На прямой выбраны четыре точки A, B, C и D, причем AB = 1, BC = 2, CD = 4. Чему может быть равно AD? Укажите все возможные варианты.
Anonymous Poll
62%
1
10%
2
66%
3
14%
4
65%
5
11%
6
75%
7
5%
8
4%
9
10%
не хватает правильных вариантов
Forwarded from Фулл и точка
Открываем рубрику #красота_спасет_мир 🥳
Здесь мы будем предлагать вам задачи с простым и неожиданным решением, не требующим глубоких знаний💡
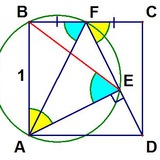
Дан шестиугольник 𝐴𝐵𝐶𝐷𝐸𝐹, в котором 𝐴𝐵 = 𝐵𝐶, 𝐶𝐷 = 𝐷𝐸, 𝐸𝐹 = 𝐹𝐴, а углы 𝐴 и 𝐶 — прямые. Докажите, что прямые 𝐹𝐷 и 𝐵𝐸 перпендикулярны.
Здесь мы будем предлагать вам задачи с простым и неожиданным решением, не требующим глубоких знаний💡
Дан шестиугольник 𝐴𝐵𝐶𝐷𝐸𝐹, в котором 𝐴𝐵 = 𝐵𝐶, 𝐶𝐷 = 𝐷𝐸, 𝐸𝐹 = 𝐹𝐴, а углы 𝐴 и 𝐶 — прямые. Докажите, что прямые 𝐹𝐷 и 𝐵𝐸 перпендикулярны.
Forwarded from Геометрия от Волчкевича
Путь из точки А в точку В
Пару месяцев назад редакция журнала Тинькофф—образование взяла у меня интервью. В нем я ответил на много вопросов: почему я стал учителем, зачем написал учебник, какие задачи интересны детям, что делаю в свободное от работы время, какие математические модели можно потрогать руками, нужна ли история науки в школе, работает ли сейчас социальный лифт в образовании.
Это интервью вышло пару дней назад. Вот ссылка на него:
https://j.tinkoff.ru/e-tg/maths-schoolbook/
Кстати, в комментариях к этому интервью развернулась целая дискуссия о пользе геометрии в школьном образовании.
Пару месяцев назад редакция журнала Тинькофф—образование взяла у меня интервью. В нем я ответил на много вопросов: почему я стал учителем, зачем написал учебник, какие задачи интересны детям, что делаю в свободное от работы время, какие математические модели можно потрогать руками, нужна ли история науки в школе, работает ли сейчас социальный лифт в образовании.
Это интервью вышло пару дней назад. Вот ссылка на него:
https://j.tinkoff.ru/e-tg/maths-schoolbook/
Кстати, в комментариях к этому интервью развернулась целая дискуссия о пользе геометрии в школьном образовании.
Т—Ж
Как я пишу учебники по геометрии
История учителя, который любит составлять задачи
Forwarded from Математический конструктор
This media is not supported in your browser
VIEW IN TELEGRAM
Если равенство треугольников, как правило, можно установить по их трем соответственным элементам, то по таким трем элементам треугольник можно и восстановить, не так ли? Именно поэтому три признака равенства треугольников легко превращаются в три задачи на построение – но всегда ли у них будет одно решение?
Приглашаем вас в математическую лабораторию, где на динамических чертежах можно провести построение сразу для всех возможных значений данных – изменяйте эти значения, и вместе с ними будет меняться чертеж. Проведите полноценное исследование задачи на построение и выясните, в каких случаях решения не окажется.
Первый признак равенства
Второй признак равенства
Третий признак равенства
#Матконструктор
#Математический_конструктор
Приглашаем вас в математическую лабораторию, где на динамических чертежах можно провести построение сразу для всех возможных значений данных – изменяйте эти значения, и вместе с ними будет меняться чертеж. Проведите полноценное исследование задачи на построение и выясните, в каких случаях решения не окажется.
Первый признак равенства
Второй признак равенства
Третий признак равенства
#Матконструктор
#Математический_конструктор
«В любом школьном учебнике геометрии вы найдёте три признака равенства треугольников. А верен ли четвёртый признак: по двум сторонам и углу, лежащему напротив одной из них? Не обязательно! Вот простой пример…»
— но примером эта небольшая статья А.Д.Блинкова про «четвертый признак равенства треугольников» не заканчивается, а только начинается
https://old.kvantik.com/art/files/pdf/2020-01.18-21.pdf
— но примером эта небольшая статья А.Д.Блинкова про «четвертый признак равенства треугольников» не заканчивается, а только начинается
https://old.kvantik.com/art/files/pdf/2020-01.18-21.pdf
Дан треугольник, два угла которого равны 25° и 80°. Докажите, что в нём биссектриса какого-то угла и одна из трисектрис какого-то угла перпендикулярны друг другу.
Эту задачу не надо обсуждать в комментариях, потому что она из первого тура заочного конкурса журнала «Квантик». Лучше предложите ее знакомым ученикам 5–8 классов.
Подробнее о конкурсе и остальные задачи: https://tttttt.me/kvantik12/377
Эту задачу не надо обсуждать в комментариях, потому что она из первого тура заочного конкурса журнала «Квантик». Лучше предложите ее знакомым ученикам 5–8 классов.
Подробнее о конкурсе и остальные задачи: https://tttttt.me/kvantik12/377