Please open Telegram to view this post
VIEW IN TELEGRAM
В пятиугольнике ABCDE площади треугольников ABC, BCD, CDE, DEA и EAB равны a, b, c, d и e. Доказать, что площадь всего пятиугольника является корнем уравнения
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
Forwarded from Геометрия с Ниловым
Задача про луночки Альхазена (https://ru.wikipedia.org/wiki/%D0%98%D0%B1%D0%BD_%D0%B0%D0%BB%D1%8C-%D0%A5%D0%B0%D0%B9%D1%81%D0%B0%D0%BC).
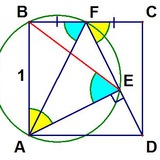
На катете AB прямоугольного треугольника ABC во внешнюю сторону построили красную полуокружность. Вместе с красной дугой AB описанной окружности треугольника ABC они образуют красную луночку (ограниченную двумя красными дугами). Аналогично поступили с катетом BC и получили зеленую луночку. Докажите, что площади красной и зеленой луночек равны половине площади треугольника ABC.
Теперь в обе луночки вписали окружности наибольшего возможного радиуса. Докажите, что радиусы этих окружностей равны половине радиуса вписанной окружности треугольника ABC.
На катете AB прямоугольного треугольника ABC во внешнюю сторону построили красную полуокружность. Вместе с красной дугой AB описанной окружности треугольника ABC они образуют красную луночку (ограниченную двумя красными дугами). Аналогично поступили с катетом BC и получили зеленую луночку. Докажите, что площади красной и зеленой луночек равны половине площади треугольника ABC.
Теперь в обе луночки вписали окружности наибольшего возможного радиуса. Докажите, что радиусы этих окружностей равны половине радиуса вписанной окружности треугольника ABC.
а) Доказать, что для любых 4 векторов на плоскости выполняется соотношение типа Птолемея/Плюккера:
s(12)s(34)-s(13)s(24)+s(14)s(23)=0,
где s(ij) — ориентированная площадь натянутого на вектора i и j треугольника.
б) Вывести отсюда утверждение https://tttttt.me/geometrykanal/2499 про площадь пятиугольника.
s(12)s(34)-s(13)s(24)+s(14)s(23)=0,
где s(ij) — ориентированная площадь натянутого на вектора i и j треугольника.
б) Вывести отсюда утверждение https://tttttt.me/geometrykanal/2499 про площадь пятиугольника.
Telegram
Геометрия-канал
В пятиугольнике ABCDE площади треугольников ABC, BCD, CDE, DEA и EAB равны a, b, c, d и e. Доказать, что площадь всего пятиугольника является корнем уравнения
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
Трисекция углов с помощью некоторых коник. По мотивам проекта про трисекцию на последнем ЛКТГ.
Forwarded from NeuroGeometry (Петр Ким)
Хотели бы сделать объявление:
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.
Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду
Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+
При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии
От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!
https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.
Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду
Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+
При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии
От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!
https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced
а4) Четырехугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда четырехугольник можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения противоположных сторон всё время лежат на одной прямой.
б4) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).
// via П.Бибиков: https://vk.com/wall840911_606
б4) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).
// via П.Бибиков: https://vk.com/wall840911_606
а5) Пятиугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда его можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения продолжений сторон всё время лежат на одной конике.
б5) Полный пятисторонник вписан в квартику. Доказать, что его можно “вращать” с сохранением вписанности — и что все такие пятисторонники касаются одной коники (предыдущий пункт соответствует квартике, распадающейся в объединение двух коник). // Lüroth, 1868
Upd: и дальше то же самое, говорят ; (Дарбу)
б5) Полный пятисторонник вписан в квартику. Доказать, что его можно “вращать” с сохранением вписанности — и что все такие пятисторонники касаются одной коники (предыдущий пункт соответствует квартике, распадающейся в объединение двух коник). // Lüroth, 1868
Upd: и дальше то же самое, говорят ; (Дарбу)
у коллег из GetAClass вышел новый ролик,
https://youtu.be/oA7-_0eHdp8
«Представьте себе, что вы взяли обычный прямой круговой конус — тот, что вы изучали в школе — и нарезали его на тонкие круговые дольки параллельно основанию. А теперь сдвиньте эти дольки равномерно относительно друг друга, и у вас получится косой круговой конус.
И вот оказывается, что этот наклонный конус можно нарезать на круговые дольки вторым способом, рассекая его другим семейством плоскостей под углом к основанию!
Попробуйте догадаться, как это сделать, а потом доказать, что в сечениях действительно получаются круги…»
https://youtu.be/oA7-_0eHdp8
«Представьте себе, что вы взяли обычный прямой круговой конус — тот, что вы изучали в школе — и нарезали его на тонкие круговые дольки параллельно основанию. А теперь сдвиньте эти дольки равномерно относительно друг друга, и у вас получится косой круговой конус.
И вот оказывается, что этот наклонный конус можно нарезать на круговые дольки вторым способом, рассекая его другим семейством плоскостей под углом к основанию!
Попробуйте догадаться, как это сделать, а потом доказать, что в сечениях действительно получаются круги…»
Forwarded from Геометрия с Ниловым
Отличная книжка про коники. Лучше смотреть 2 издание, но не нашел его в свободном доступе.
https://old.mccme.ru/free-books/akopyan/Zaslavky-Akopyan.pdf
https://old.mccme.ru/free-books/akopyan/Zaslavky-Akopyan.pdf
Было бы также интересно посмотреть на статистику по другим олимпиадам.
https://habr.com/ru/articles/837336/
https://habr.com/ru/articles/837336/
Хабр
Стала ли AlphaGeometry прорывом в ИИ?
Примерно полгода назад математическое сообщество услышало новость о том, что исследователи DeepMind создали ИИ-систему, решающую геометрические задачи с Международной математической олимпиады на...
Было бы интересно сделать подборку сюжетов, в которых геометрия переплетается с физикой. Если кто-то знает нестандартные - напишите в комментах
Forwarded from Непрерывное математическое образование
YouTube
Удивительная связь физики и геометрии!
Может ли классическая механика и законы оптики выручить в сложных геометрических задачах? Трудно представить, но бывает и такое!
Поддержите канал Wild Mathing! https://boosty.to/wildmathing
Мои курсы: https://vk.com/market-135395111
VK: https://vk.com/wildmathing…
Поддержите канал Wild Mathing! https://boosty.to/wildmathing
Мои курсы: https://vk.com/market-135395111
VK: https://vk.com/wildmathing…