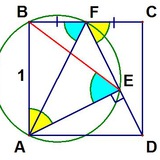
а) Доказать, что для любых 4 векторов на плоскости выполняется соотношение типа Птолемея/Плюккера:

s(12)s(34)-s(13)s(24)+s(14)s(23)=0,

где s(ij) — ориентированная площадь натянутого на вектора i и j треугольника.

б) Вывести отсюда утверждение https://tttttt.me/geometrykanal/2499 про площадь пятиугольника.

Хотели бы сделать объявление:
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.

Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду

Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+

При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии

От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!

https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced

а4) Четырехугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда четырехугольник можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения противоположных сторон всё время лежат на одной прямой.

б4) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).

// via П.Бибиков: https://vk.com/wall840911_606

а5) Пятиугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда его можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения продолжений сторон всё время лежат на одной конике.

б5) Полный пятисторонник вписан в квартику. Доказать, что его можно “вращать” с сохранением вписанности — и что все такие пятисторонники касаются одной коники (предыдущий пункт соответствует квартике, распадающейся в объединение двух коник). // Lüroth, 1868

Upd: и дальше то же самое, говорят ; (Дарбу)

Треугольник правильный. Круг произвольный. Доказать, что синяя длина равна красной

// задача от Произволова

у коллег из GetAClass вышел новый ролик,
https://youtu.be/oA7-_0eHdp8

«Представьте себе, что вы взяли обычный прямой круговой конус — тот, что вы изучали в школе — и нарезали его на тонкие круговые дольки параллельно основанию. А теперь сдвиньте эти дольки равномерно относительно друг друга, и у вас получится косой круговой конус.

И вот оказывается, что этот наклонный конус можно нарезать на круговые дольки вторым способом, рассекая его другим семейством плоскостей под углом к основанию!

Попробуйте догадаться, как это сделать, а потом доказать, что в сечениях действительно получаются круги…»

Отличная книжка про коники. Лучше смотреть 2 издание, но не нашел его в свободном доступе.

https://old.mccme.ru/free-books/akopyan/Zaslavky-Akopyan.pdf

Было бы также интересно посмотреть на статистику по другим олимпиадам.

https://habr.com/ru/articles/837336/

А вот и второе издание.

Для окружности радиус в точку касания перпендикулярен касательной.

А что для эллипса: как связаны отрезок из фокуса в точку касания и перпендикуляр из фокуса на касательную? Простая задача: доказать, что красные отрезки параллельны.

// via Д.А.Терёшин via Stanley Rabinowitz

Было бы интересно сделать подборку сюжетов, в которых геометрия переплетается с физикой. Если кто-то знает нестандартные - напишите в комментах

https://youtu.be/J4yDkZ0Z6Qo

физические соображения в геометрических задачах от Wild Mathing

Задача для любителей изогонального сопряжения. Зеленая и оранжевая точки являются изогонально сопряженными точке P относительно треугольников соответственного цвета. Докажите, что красные углы равны

Как мы говорили раньше, коники иногда неожиданно помогают придумать классное и короткое решение сложной задачи 💪
Так случилось на летней школе в Казани с одной из задач по мотивам проекта ЛКТГ-2015, которая была в листике Павла Александровича Кожевникова.

Участник нашего проекта и наш подписчик Иванов Госман придумал ранее неизвестное крутое решение при помощи поляр и гиперболы F (о которой см. предыдущий пост).

Поздравляем Госмана 🥳

Публикуем условие задачи. Подумайте над ней и вы 🤔

Вдруг родится еще одна новая идея 💡

Задача. В остроугольном треугольнике 𝐴𝐵𝐶 проведены высоты 𝐴𝐻𝑎, 𝐵𝐻𝑏 и 𝐶𝐻𝑐.
Точки I и O — соответственно центры вписанной и вневписанной окружностей.
Докажите, что если I лежит на 𝐻𝑏𝐻𝑐, то прямая OI проходит через 𝐻𝑎.

в личные сообщения написали вопрос, где можно прочитать про применения выхода в комплексные числа в вещественной геометрии — мб что-нибудь посоветуете?

(имеется в виду не параметризация точек плоскости комплексными числами, а выход из R(P)² в C(P)² — e.g. радикальная ось как вещественная прямая через две комплексные точки пересечения, общие точки всех окружностей, афф. эквивалентность гипербол и окружностей [над C] и проч.)