Forwarded from JustScience | Олимпиадная Математика (Вова)
#Геометрия #Задача
Через точку внутри окружности Ω проведены три хорды, делящие ее на шесть криволинейных треугольников. В три из них, через один, вписали оранжевые окружности. Докажите, что сумма радиусов оранжевых окружностей не превосходит радиуса Ω.
Обсудить решение вы можете в нашем чате!
Через точку внутри окружности Ω проведены три хорды, делящие ее на шесть криволинейных треугольников. В три из них, через один, вписали оранжевые окружности. Докажите, что сумма радиусов оранжевых окружностей не превосходит радиуса Ω.
Обсудить решение вы можете в нашем чате!
Геометрия-канал
Добрая задача. Докажите,что сумма площадей нечетных треугольников равна сумма площадей четных треугольников. (Одноцветные четырехугольники являются квадратами)
Интересно посмотреть, верно ли такое: если для четноугольника суммы площадей четных и нечетных треугольников равны для первого слоя, то аналогичное равенство сумм площадей четырехугольников будет верно и для всех слоев
Forwarded from Олимпиадная геометрия
Из комментариев от пользователя Yu Ka. Красный и синий треугольники правильные. Доказать, что зеленый тоже правильный.
Forwarded from Геометрия с Ниловым
Симпатичная несложная "учебная" задача моего учителя М.А. Волчкевича. Попробуйте решить ее в уме.
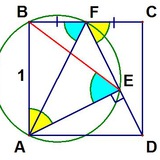
В параллелограмме ABCD точка E – середина AD. Точка F – основание перпендикуляра, опущенного из B на прямую CE.
Докажите, что треугольник ABF – равнобедренный.
Рекомендую к прочтению его учебники Матвертикали 7-9, зеленый задачник Геометрия 7-8 и канал @volk_geometry
В параллелограмме ABCD точка E – середина AD. Точка F – основание перпендикуляра, опущенного из B на прямую CE.
Докажите, что треугольник ABF – равнобедренный.
Рекомендую к прочтению его учебники Матвертикали 7-9, зеленый задачник Геометрия 7-8 и канал @volk_geometry
Forwarded from AllМАT
Вот такая интересная задача мне попалась на днях: AD — биссектриса, J — точка на отрезке AD,
P — пересечение касательной к (АКL) в точке А и ВС. Докажите, что Р равноудалена от А и J.
Источник: устный тур «ТурГор» 2019, 6 задача.
Ждем ваши решения в комментариях!💪
Вот и весь AllМАТ🟣
P — пересечение касательной к (АКL) в точке А и ВС. Докажите, что Р равноудалена от А и J.
Источник: устный тур «ТурГор» 2019, 6 задача.
Ждем ваши решения в комментариях!
Вот и весь AllМАТ
Please open Telegram to view this post
VIEW IN TELEGRAM
Forwarded from Олимпиадная математика ВсОШ | Дабромат
⬜️ Финал олимпиады им. Шарыгина
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Федорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Федоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Федорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Федоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Геометрия-канал
Photo
Отмечу крутую задачу от Григория Забазнова, а именно 9.8. Точки P и Q изогонально сопряжены в треугольнике ABC.
Forwarded from Григорий Забазнов
Isogonal_conjugate_points__To_prove_circle_through_4_points.pdf
361 KB
Forwarded from Григорий Забазнов
Более подробно решение, которое упомянул Петя Ким, можно прочитать в файлике выше
Please open Telegram to view this post
VIEW IN TELEGRAM
В пятиугольнике ABCDE площади треугольников ABC, BCD, CDE, DEA и EAB равны a, b, c, d и e. Доказать, что площадь всего пятиугольника является корнем уравнения
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
S² −S(a+b+c+d+e)+(ab+bc+cd+de+ea)=0.
// задачу предложил Мёбиус в 1823 году
Forwarded from Геометрия с Ниловым
Задача про луночки Альхазена (https://ru.wikipedia.org/wiki/%D0%98%D0%B1%D0%BD_%D0%B0%D0%BB%D1%8C-%D0%A5%D0%B0%D0%B9%D1%81%D0%B0%D0%BC).
На катете AB прямоугольного треугольника ABC во внешнюю сторону построили красную полуокружность. Вместе с красной дугой AB описанной окружности треугольника ABC они образуют красную луночку (ограниченную двумя красными дугами). Аналогично поступили с катетом BC и получили зеленую луночку. Докажите, что площади красной и зеленой луночек равны половине площади треугольника ABC.
Теперь в обе луночки вписали окружности наибольшего возможного радиуса. Докажите, что радиусы этих окружностей равны половине радиуса вписанной окружности треугольника ABC.
На катете AB прямоугольного треугольника ABC во внешнюю сторону построили красную полуокружность. Вместе с красной дугой AB описанной окружности треугольника ABC они образуют красную луночку (ограниченную двумя красными дугами). Аналогично поступили с катетом BC и получили зеленую луночку. Докажите, что площади красной и зеленой луночек равны половине площади треугольника ABC.
Теперь в обе луночки вписали окружности наибольшего возможного радиуса. Докажите, что радиусы этих окружностей равны половине радиуса вписанной окружности треугольника ABC.