Forwarded from Kvantland | Квантландия | Интересные задачи и не только
В этом году на базовом Турнире Городов в феврале было целых две задачи-картинки и обе от авторов Квантландии. Сегодня первая из них:
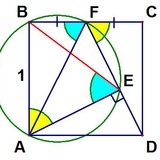
Произвольный прямоугольник разбит на прямоугольные треугольники так, как показано на рисунке ниже. В каждый треугольник вписан квадрат. Что больше: площадь красного квадрата или сумма площадей трёх зелёных?
Произвольный прямоугольник разбит на прямоугольные треугольники так, как показано на рисунке ниже. В каждый треугольник вписан квадрат. Что больше: площадь красного квадрата или сумма площадей трёх зелёных?
Forwarded from Олимпиадная геометрия
Finally... Завтра 8-го марта с 17-00 до 21-00 по московскому времени я буду решать задачи заочного тура олимпиады Шарыгина.
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
YouTube
#9str. Прорешиваем заочный тур олимпиады Шарыгина 2024
В этом стриме мы будем прорешивать задачи заочного тура олимпиады Шарыгина, который завершился на днях. Я буду делать это без предварительной подготовки в режиме онлайн.
На боковых сторонах AB и BC равнобедренного остроугольного треугольника берут такие точки M и K, что угол MEA равен углу ABC (E — пересечение CM и AK). Доказать, что середины всевозможных отрезков MK лежат на одной прямой.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
Попробую сделать традицией выкладывать решения из чата в канал. Решение обобщение задачи выше.
Forwarded from Денис Егоров
Please open Telegram to view this post
VIEW IN TELEGRAM
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2024/2024_zaoch_rus_sol.pdf
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
Forwarded from Kvantland | Квантландия | Интересные задачи и не только
А теперь вторая задача-картинка от авторов Квантландии (Е. Бакаев), которая совсем недавно была на базовом Турнире Городов:
Пять равносторонних треугольников расположены так, как показано на рисунке ниже. Три больших треугольника равны между собой, и два маленьких тоже равны между собой. Найдите углы треугольника ABC.
Пять равносторонних треугольников расположены так, как показано на рисунке ниже. Три больших треугольника равны между собой, и два маленьких тоже равны между собой. Найдите углы треугольника ABC.
На плоскости нарисовали несколько окружностей, после чего отметили все точки их пересечения или касания. Оказалось, что на каждой окружности лежит ровно n отмеченных точек и через каждую отмеченную точку проходит ровно n окружностей. Чему может быть равно n?