Forwarded from Быстрые задачки по математике (Alexey Sgibnev)
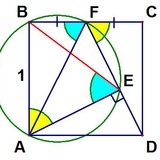
Диагонали четырёхугольника перпендикулярны и он вписан в окружность. Тогда это…
Anonymous Quiz
22%
только квадрат
22%
только квадрат или равнобедренная трапеция
56%
не обязательно квадрат или равнобедренная трапеция
(из «Олимпиадной геометрии»): красные окружности равны — доказать, что и синие окружности равны
(кроме того, что просто нравится) кажется еще похожим на обсуждавшуюся раньше “теорему о четырех кругах” — можно попробовать перенесети решение, или смешать два утверждения и т.п.
(кроме того, что просто нравится) кажется еще похожим на обсуждавшуюся раньше “теорему о четырех кругах” — можно попробовать перенесети решение, или смешать два утверждения и т.п.
Геометрия-канал
(из «Олимпиадной геометрии»): красные окружности равны — доказать, что и синие окружности равны (кроме того, что просто нравится) кажется еще похожим на обсуждавшуюся раньше “теорему о четырех кругах” — можно попробовать перенесети решение, или смешать два…
обобщение (включающее и предыдущую задачу, и теорему о четырех кругах) от коллеги Нилова: если зеленые окружности равны, то и остальные окружности (попарно) равны
а если и не равны — то линии центров (по одной для каждого цвета) все пересекаются на стороне треугольника
https://www.geogebra.org/classic/m8fv5jpn
а если и не равны — то линии центров (по одной для каждого цвета) все пересекаются на стороне треугольника
https://www.geogebra.org/classic/m8fv5jpn
Forwarded from Sergey Markelov
Существует ли такая выпуклая фигура на плоскости, которую можно поделить на 7 равновеликих по площади частей 3 прямыми?
(источник)
Что-то у меня не получается решить.
(источник)
Что-то у меня не получается решить.
Forwarded from Непрерывное математическое образование
https://www.youtube.com/live/uyPtQqHSjUA
видеозапись рассказа Наталии Стрелковой про степени свободы и т.п. в геометрии
видеозапись рассказа Наталии Стрелковой про степени свободы и т.п. в геометрии
YouTube
2023/24. Лекция 12. "Пошевелим геометрию и стереометрию"
Спикер: Стрелкова Наталия Павловна, учитель математики школы 179
Как решить геометрическую задачу? Бывает полезно понять, какие есть степени свободы у конструкции. Какие ограничения наложены условиями задачи. Все ли их мы уже учли. Выдвинуть гипотезы и проверить…
Как решить геометрическую задачу? Бывает полезно понять, какие есть степени свободы у конструкции. Какие ограничения наложены условиями задачи. Все ли их мы уже учли. Выдвинуть гипотезы и проверить…
1) Даны две окружности с общим центром. Построить одной линейкой этот центр.
2) Даны две пересекающиеся окружности. Построить одной линейкой их общие касательные.
2) Даны две пересекающиеся окружности. Построить одной линейкой их общие касательные.
В равностороннем треугольнике ABC отметили точки N, K, M на сторонах AB, BC, AC соответственно так, что AM = 1, BN = 2, BK= 3, CM= 4. Докажите, что треугольник MNK равнобедренный.
Задача из 6-го этапа заочного конкурса журнала «Квантик»: https://tttttt.me/kvantik12/317
Не обсуждайте, пожалуйста, решение.
Задача из 6-го этапа заочного конкурса журнала «Квантик»: https://tttttt.me/kvantik12/317
Не обсуждайте, пожалуйста, решение.
Из точки M внутри правильного треугольника ABC сторона видна под углом 150 градусов. Доказать, что из отрезков MA, MB, MC можно составить прямоугольный треугольник.
Замостите плоскость одинаковыми плитками, граница каждой из которых состоит из трёх дуг окружностей, имеющих общие концы.
Могут ли эти дуги быть попарно различными? Как описать все такие замощения?
Могут ли эти дуги быть попарно различными? Как описать все такие замощения?
Forwarded from Геометрия от Волчкевича
Круги в квадрате.
Древние греки не могли решить некоторые задачи с помощью циркуля и линейки. Самыми известными из них были задачи об удвоении куба, деление произвольного угла на три равные части, построение правильного семиугольника и квадратура круга.
Только в XIX веке было доказано, что циркулем и линейкой из единичного отрезка можно построить лишь квадратичные иррациональности, то есть все числа, которые получаются из 1 с помощью арифметических операций и извлечения квадратных корней. Кстати, это доказательство вполне доступно школьникам.
Корни большинства кубических уравнений (если среди них нет рациональных) нельзя представить в таком виде, поэтому и построить их классическими инструментами не получится.
Вашему вниманию предлагается задача о трех равных кругах в квадрате, которую тоже не решить циркулем и линейкой, ведь радиус нужных кругов - корень кубического уравнения с целыми коэффициентами.
Какое это должно быть уравнение?
Древние греки не могли решить некоторые задачи с помощью циркуля и линейки. Самыми известными из них были задачи об удвоении куба, деление произвольного угла на три равные части, построение правильного семиугольника и квадратура круга.
Только в XIX веке было доказано, что циркулем и линейкой из единичного отрезка можно построить лишь квадратичные иррациональности, то есть все числа, которые получаются из 1 с помощью арифметических операций и извлечения квадратных корней. Кстати, это доказательство вполне доступно школьникам.
Корни большинства кубических уравнений (если среди них нет рациональных) нельзя представить в таком виде, поэтому и построить их классическими инструментами не получится.
Вашему вниманию предлагается задача о трех равных кругах в квадрате, которую тоже не решить циркулем и линейкой, ведь радиус нужных кругов - корень кубического уравнения с целыми коэффициентами.
Какое это должно быть уравнение?
Геометрия-канал
SAGF 2024 SL 1. Сколько парабол можно провести через вершины треугольника так, что ее фокус лежит на описанной окружности?
В продолжение этого сюжета. Ответ: 6. Можно доказать,что фокусы этих парабол являются точками пересечения вневписанных окружностей с описанной окружностью. Предлагается доказать это и то,что каждая парабола содержит одну из внешних точек Жергонна.
Forwarded from Vladimir Dubrovsky
Задача о делении на равные части сгибанием была осенью у нас на Турнире по математическому моделированию https://internat.msu.ru/media/uploads/2023/10/omarstarsh2023resheniya.pdf. В задачах на сгибание надо точно указывать разрешенные операции. "Простые" операции - сложить по линии через две имеющиеся точки или так, чтобы совместить две точки. А при "удвоении куба" предлагается поместить одну точку на одну линию, а другую - на другую линию. Это примерно то же самое, что и метод вставки Архимеда при трисекции угла, позволяющий решать кубические уравнения. Так что ничего удивительного.
Дан стандартный лист бумаги А4. Сложите из него а) квадрат; б) правильный треугольник; в) правильный пятиугольник; г) правильный нечетноугольник. Можно ли сложить правильный восьмиугольник?
Геометрия-канал
Замостите плоскость одинаковыми плитками, граница каждой из которых состоит из трёх дуг окружностей, имеющих общие концы. Могут ли эти дуги быть попарно различными? Как описать все такие замощения?
2024-02-12 20.43.27.jpg
149.2 KB
Два разных замощения плитками, граница которых состоит из полуокружности и двух четвертинок.