Задачи на каникулы

Чем можно заняться на Новогодней неделе? Доесть праздничный салат, сходить в гости, покататься на коньках… Хотя в такой мороз последнее — это отчаянный поступок. Уж лучше сесть у горящего камина в качающееся кресло и открыть хорошую книгу. А еще лучше порешать хорошие геометрические задачи — это я и предлагаю вам сделать :)

Пять задач на этом новогоднем листке я выдал ученикам своего девятого класса как задание на зимние каникулы. Правда, оно для них необязательное. Там есть и сложные задачи, но главное — все они новые, с ответами и не гуглятся (извините за новомодное слово).

Как обычно, пишите в чат только ответы, а не решения :)
Хорошего вам проведения времени и раздумий!

синие окружности проходят через одну точку — доказать, что и красные окружности проходят через одну точку

// конечно, это просто точка Микеля после инверсии — но просто картинка нравится…

синие окружности проходят через одну точку — доказать, что красные окружности проходят через одну точку. (Еще немного Микеля, но другого.)

Всем полуночный привет! Очень-очень важная новость для любителей геометрии, красивых геометрических задач и вообще всякой геометрической нетривиальщины.

Открылась регистрация на онлайн геометрическую олимпиаду SAGF-2024.
- Эта олимпиада из 8 задач, в которой может участвовать любой желающий (имеющий аккаунт на aopse), а может даже команда до 3 человек.
- Решения можно присылать на русском, английском или китайском языке
- Можно пользоваться геогеброй, ну и вообще чем пожелаете
- На решение каждой из двух частей отводится три дня

Будет сложно? Сложность соответствует задачам из шорт-листа

P1/P5 G3-G4
P2/P6 G5
P3/P7 G6-G8
P4/P8 G8+.

Мне выпала честь уже посмотреть на задачи и среди них есть просто супер-пупер геометрии!

Если вы хотите поучаствовать, переходите по ссылке и регистрируйтесь! Задачи прошлого года можно найти тут.

https://mccme.ru/nir/seminar/

в четверг (11.01) продолжится семинар учителей математики:

А.Д.Блинков будет рассказывать про книжку «Площади без формул», которая скоро выйдет в серии «Школьные математические кружки»

как обычно: 19:00, столовая МЦНМО, приглашаются все желающие

На синей прямой выбрана точка A, а на синей окружности точка B. Через них проводят всевозможные окружности — они пересекают исходные прямую и окружность в точках X и Y.

Доказать, что все получающиеся так прямые XY проходят через фиксированную точку.

// Если вас утомило возвышенное в канале — здесь понятное решение, не требующее ничего сверх школьной программы — попробуйте!

// А если возвышенное не утомило, то эта точка называется, конечно, A+B (а задача взята из текста Заславского и Кожевникова про кубики в МатПросвещении-32).

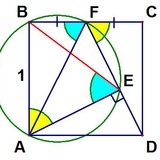
Плоская выпуклая фигура ограничена отрезками AB и AD и дугой BD некоторой окружности. Построить какую-нибудь прямую, которая делит площадь этой фигуры пополам

// задача с сегодняшнего семинара учителей

Задача — повод напомнить о прекрасной книге Б.П. Гейдмана :
https://math.ru/lib/files/pdf/mp-seria/book.9.pdf

#видео

❗️А.Д.Блинков. Площади без формул.

О новой книжке из серии “Школьные математические кружки”.

Опрос ↑↑
Источник: «Площади без формул» А.Д. Блинкова (выйдет в феврале-марте). Доклад

Все репостят новость про то, как AlphaGeomery решила 25 из 30 задач с международной олимпиады. Если вы еще не видели, то вот: https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/

Что думаете?

наверное у всех, кто интересовался теоремой Понселе, возникало желание строить вписанно-описанные (неправильные) 5-угольники — но как это сделать?

https://www.geogebra.org/m/xrcdd7ya

вот модель от коллеги Нилова

Любую гладкую кривую можно увидеть, нарисовав не саму кривую, а множество касательных к ней. Понятие огибающей подробно описано в сюжете «Парабола: изонить», в котором в качестве огибающей семейства прямых возникает парабола.

Но построение касательных не такое простое дело. Продемонстрируем, как увидеть конические сечения — эллипс, гиперболу, параболу — ничего не считая и не рисуя, а просто складывая листок бумаги. Сюжет сегодняшнего Математического вторника: «Эллипс, гипербола, парабола: складывание листа бумаги» https://etudes.ru/models/conic-sections-paper-folding/ . Для эллипса и гиперболы понадобится вырезать кружок из бумаги, для параболы – просто прямоугольный лист.

Похожие картинки можно уже было видеть в миниатюрах Эллипс как огибающая, Гипербола как огибающая, Парабола как огибающая. Но в них надо уметь строить перпендикуляр к отрезку, а в указанном сегодня способе складывания листочка эта операция «зашита» в сам способ складывания.