Прокопенко_Разрезания_и_перекладывание_отрезков.pdf
1.3 MB
Дмитрий Прокопенко написал статью «Разрезания и перекладывание отрезков» (опубл. в журнале Архимед)
обсуждаются и задачи https://tttttt.me/geometrykanal/1813 и задача https://tttttt.me/geometrykanal/2269 и еще разное
«…Казалось бы, что может быть проще равностороннего треугольника? Решение вызвало смесь восхищения и удивления. Потом попадались еще задачки с похожей конструкцией. С некоторыми из них, среди которых есть настоящие шедевры, а также с характерными приемами решения мы и познакомимся…»
обсуждаются и задачи https://tttttt.me/geometrykanal/1813 и задача https://tttttt.me/geometrykanal/2269 и еще разное
«…Казалось бы, что может быть проще равностороннего треугольника? Решение вызвало смесь восхищения и удивления. Потом попадались еще задачки с похожей конструкцией. С некоторыми из них, среди которых есть настоящие шедевры, а также с характерными приемами решения мы и познакомимся…»
🔥10👍4❤1
Любопытный сайт, на котором можно найти множество геометричных орнаментов.
https://patterninislamicart.com/
https://patterninislamicart.com/
❤15👍4😁1😢1
Очень крутая задача с секретом с MMO 2021(это не Московская олимпиада, а макет в стиле IMO). Предлагалась под номером 3. Картинку не рисую. Пусть ABC - неравнобедренный треугольник. Предположим, что окружность с центром на прямой BC, проходящая через A, окружность с центром на прямой AC, проходящая через B, и окружность с центром на прямой AB,проходящая через C, имеют общую радикальную ось. Докажите, что центр описанной окружности треугольника ABC лежит на этой радикальной оси.
🔥19❤3
Wild Mathing напомнил задачу с Всесоюзной олимпиады (и статью в Кванте про нее):
Один тетраэдр лежит внутри другого. Может ли сумма длин ребер у внутреннего быть больше, чем у внешнего? Какое максимальное отношение можно получить?
(Ср., кстати, с аналогичной задачей про параллелепипеды.)
Один тетраэдр лежит внутри другого. Может ли сумма длин ребер у внутреннего быть больше, чем у внешнего? Какое максимальное отношение можно получить?
(Ср., кстати, с аналогичной задачей про параллелепипеды.)
👍13🔥1
Forwarded from Théo D'or
Я, кстати, знаю еще один прекрасный пример как "меньшее может быть большим". В свое время меня этот пример поразил до глубины души. Он, правда, про размерности выше 3.
Вопрос такой. Существует ли в n-мерном пространстве два центрально симметричных тела A и B (с центром в начале координат) таких, что площади всех (n-1)-мерных центральных сечений A меньше, чем площади соответствующих сечений B, а объем A больше объема B.
Особо удивительно то, что в размерности, начиная, кажется с 7, контрпримером служит шар и куб, и это почти совсем просто понять...
Вопрос такой. Существует ли в n-мерном пространстве два центрально симметричных тела A и B (с центром в начале координат) таких, что площади всех (n-1)-мерных центральных сечений A меньше, чем площади соответствующих сечений B, а объем A больше объема B.
👍18😱7❤3🤔2
VIKKi - Ringel Circles Problem - YouTube
https://www.youtube.com/watch?v=s-3OwgwT7qw
https://www.youtube.com/watch?v=s-3OwgwT7qw
YouTube
VIKKi - Ringel Circles Problem
In 1959 Gerhard Ringel posed the following problem which remained open for over 60 years.
Is it possible to always color a given set of circles in the plane with five colors so that tangent circles get distinct colors?
James Davis, Chaya Keller, Linda Kleist…
Is it possible to always color a given set of circles in the plane with five colors so that tangent circles get distinct colors?
James Davis, Chaya Keller, Linda Kleist…
👍11🔥1
Теорема Понселе для треугольника, четырехугольника и пятиугольника с явными параметризациями для радиусов вписанной и описанной окружностей и расстояния между их центрами.
https://www.geogebra.org/classic/bjpvtpwm
https://www.geogebra.org/classic/dx3sgmnb
https://www.geogebra.org/classic/mcfys5q6
https://www.geogebra.org/classic/bjpvtpwm
https://www.geogebra.org/classic/dx3sgmnb
https://www.geogebra.org/classic/mcfys5q6
www.geogebra.org
GeoGebra Classic - GeoGebra
Free online apps bundle from GeoGebra: get graphing, geometry, algebra, 3D, statistics, probability, all in one tool!
❤5👍2🔥2
подробный анонс: https://tttttt.me/vsosh_olymp/156
«Движение точек — мощный метод решения геометрических задач, который в последние годы стал крайне популярен (…) за счет своей кажущейся простоты и невероятной силы (…). Однако в подавляющем большинстве случаев школьники неправильно понимают концепции теории движения точек, из-за чего пишут на олимпиадах решения, содержащие серьезные ошибки.
На стриме мы поговорим об одном из самых простых видов движения — о проективном. Мы разберем несколько задач, которые в свое время считались крайне трудными, но в одну строчку решаются при помощи указанного метода. (…)
Если вы планируете участвовать в стриме, то убедитесь, что вы знаете что такое проективная прямая, проективная плоскость и двойные отношения (…).»
upd: говорят, из-за технических проблем стрим перенесели
upd2: вот, в итоге, запись —
https://www.youtube.com/live/jiZaRe1UDEM
❤13👍12
Forwarded from ppetya
Из старого дневника (2008 год), задача.
Рассмотрим круговой (это важно) конус и отсечем у него верхушку. Получится колпак (некоторый, вообще говоря не прямой, конус над эллипсом). Составим из двух таких одинаковых колпаков фигуру. Утверждается, что сумма длин образующих, соединяющих точку на эллипсе с вершинами, не зависит от точки на эллипсе. Вот это все на рисунке.
Если что -- я ее сам придумал случайно, может быть известная.
Рассмотрим круговой (это важно) конус и отсечем у него верхушку. Получится колпак (некоторый, вообще говоря не прямой, конус над эллипсом). Составим из двух таких одинаковых колпаков фигуру. Утверждается, что сумма длин образующих, соединяющих точку на эллипсе с вершинами, не зависит от точки на эллипсе. Вот это все на рисунке.
Если что -- я ее сам придумал случайно, может быть известная.
🔥15❤3👍1
ppetya
Из старого дневника (2008 год), задача. Рассмотрим круговой (это важно) конус и отсечем у него верхушку. Получится колпак (некоторый, вообще говоря не прямой, конус над эллипсом). Составим из двух таких одинаковых колпаков фигуру. Утверждается, что сумма…
Взаимосвязанный вопрос.
Дан эллипс. Найти геометрическое место вершин круговых конусов, у которых данный эллипс является сечением.
Дан эллипс. Найти геометрическое место вершин круговых конусов, у которых данный эллипс является сечением.
❤10👍2
Forwarded from Непрерывное математическое образование
https://www.geogebra.org/m/jFFERBdd#material/exrpd9dw
картинки по выходным — снова про теорему Пифагора
как собрать из (частей) правильных шестиугольников, построенных на катетах, правильный шестиугольник построенный на гипотенузе
картинки по выходным — снова про теорему Пифагора
как собрать из (частей) правильных шестиугольников, построенных на катетах, правильный шестиугольник построенный на гипотенузе
❤12👍1🥱1
Геометрия-канал
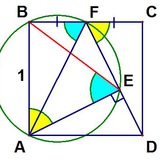
Надо доказать, что если четыре точки лежат на одной окружности, то XY диаметр этой окружности. Когда-то меня очень поразила эта задача. Попробуйте придумать авторское решение). Автор: Evan Chang, USA.
В связи с этой задачей в качестве ассоциации возникла такая классическая конструкция.
На плоскости даны 4 прямые общего положения. Для каждой пары данных прямых провели две биссекторные прямые. После чего отметили их точки пересечения. Какие точки пересечения выстраиваются на окружности и что про эти окружности можно сказать?
На плоскости даны 4 прямые общего положения. Для каждой пары данных прямых провели две биссекторные прямые. После чего отметили их точки пересечения. Какие точки пересечения выстраиваются на окружности и что про эти окружности можно сказать?
👍7❤4
Forwarded from Я веду кружок (Grigory Merzon)
Дима Швецов и Митя Мухин выложили видеозаписи докладов конференции Блинков-70
вот, например, Наташа Стрелкова рассказывает про интересный формат геометрического марафона: https://youtu.be/O6jj9Qgi13c
( весь плейлист: https://www.youtube.com/playlist?list=PLIu8Mui0KEFd4OPkgVXeQgo8Unh3bK33b )
вот, например, Наташа Стрелкова рассказывает про интересный формат геометрического марафона: https://youtu.be/O6jj9Qgi13c
( весь плейлист: https://www.youtube.com/playlist?list=PLIu8Mui0KEFd4OPkgVXeQgo8Unh3bK33b )
YouTube
Геометрический марафон
Наталия Павловна Стрелкова, учитель школы №179, рассказала о том как можно организовать повторение/изучение курса планиметрии в старших классах.
Доклад был прочитан 16 декабря 2023 в г. Москва.
https://geometry.ru/ad_70.html
Организаторы -- Митя & Дима.…
Доклад был прочитан 16 декабря 2023 в г. Москва.
https://geometry.ru/ad_70.html
Организаторы -- Митя & Дима.…
❤11🔥3👍2👎1🤔1
В этом году RMM порадовала красивой геометрической задачей. Вот ещё одна красивая задача с шорт-листа прошлого года RMM SL 2023 G3. Дан треугольник ABC и точка P. Точки O_a,O_b,O_c - центры окружностей (PBC),(PAC),(PAB) соответственно. Точка Q симметрична точке P относительно общей хорды окружностей (O_aO_bO_c) и (ABC). Докажите, что точки P и Q изогонально сопряжены в треугольнике ABC.
👍13❤5🤩4🔥1😱1