#реклама

До ЕГЭ 2 месяца! Думаешь, уже невозможно успеть подготовиться?

ВыСОТКА — это идеальное решение! За 1 месяц мы объясним то, что не смогла школа за 11 лет.

Подписывайся на наш канал, чтобы поднять бал до 100 за месяц и поступить в ВУЗ мечты🏆

В 🎁 за подписку ты получишь разбор САМЫХ сложных заданий досрочного ЕГЭ 2023 с подробными комментариями эксперта🔝

С нами у тебя еще есть время на подготовку. Не паникуй, подписывайся. Вместе мы справимся!

https://olympiads.mccme.ru/ustn/

появились задачи и решения проходившей в воскресенье устной олимпиады по геометрии

вот такая задача, например:

Есть квадратный лист бумаги. Как получить прямоугольный лист бумаги с отношением сторон, равным √2? (Инструментов никаких нет, лист можно только сгибать.)

Сегодня будет немного задач от подписчиков)

Некоторое время назад мне написал Тимур Гизатуллин. Он участвует в организации и проведении олимпиады памяти Сайяра Утяганова в Казани (ссылка на канал олимпиады в комментариях). Сайяр один из основоположников олимпиадно-математического движения в Татарстане. И вот его ученики организовались и проводят уже второй год олимпиаду, на которую сами и придумывают задачи. И мне кажется, что это просто здорово!

Одна из задач Тимура предлагалась в 9-ом классе. Вот ее условие.

В треугольник ABC (AB > BC) вписана окружность, касающаяся его сторон BC, CA и AB в точках D, E и F соответственно. Пусть ω — окружность, описанная около треугольника ABC. Точка M — середина
отрезка AF, точка N — середина отрезка CD. Окружность, описанная около треугольника BMN, пересекает ω в точках B и K. Биссектриса угла ABC пересекает ω в точках B и L. Докажите, что точки K, E и L лежат на одной прямой.

https://olympiads.mccme.ru/vmo/

появляются задачи и решения финала всероссийской олимпиады по математике (пока — первого дня)

Каждую из сторон треугольника повернули на 120 градусов вокруг центра описанной окружности. И рассмотрели пересечение каждой из сторон с её образом. Доказать, что эти точки — вершины треугольника, равного исходному.

(задача Л.Емельянова на Всеросе сегодня)

#реклама

Математическая стипендия от Школы Le Sallay Диалог покрывает 100% годовой стоимости обучения, а также полный пансион во время очных сессий (8 недель в году). Ориентирована на учеников, которые интересуются математикой и демонстрируют успехи в этой дисциплине.

✅ Школа Le Sallay Диалог — частная средняя школа (от 10 до 14 лет), работает в формате смешанного обучения, онлайн-уроки сочетаются с выездными очными сессии в Турции 4 раза в год.

✅ Школа готовит учеников к продолжению обучения в любых англоязычных high-school. Обучение по международной программе, сильная команда учителей с современными взглядами на образование, индивидуальный подход и обучение в малых группах. В школу можно перейти даже в середине учебного года.
✅ Стипендиат будет учиться в самой сильной математической группе!

*️⃣ Узнать условия и подать заявку на стипендию можно здесь.

А.Акопян задает в фб вопрос: знаете ли вы какое-нибудь доказательство трехмерной теоремы Пифагора не использующее индукцию или скалярное произведение?

(Хочется не применить две плоские теоремы Пифагора последовательно, а придумать хорошее геометрическое рассуждение в духе тех, которыми мы доказываем т. Пифагора на плоскости.)

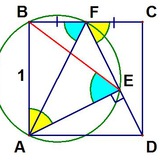
По мотивам одной задачи...

Красные углы равны, синие углы равны. Доказать, что окружности равны.

Другой вариант задачи выше, отвечающий на вопрос, что это за чевиана, которая делит треугольник на два с равными радиусами вписанной окружности.

Прямая, проходящая через основания двух высот, пересекает продолжение стороны треугольника в точке T. Доказать, что прямая TH перпендикулярна медиане.

#реклама

18 мая онлайн-университет творческих профессий «Муза» проведет День открытых дверей первого в России детского кампуса от лаборатории Sber AI, Sber AR/VR lab, Московской центральной художественной школы и Мастерской Брусникина.

Ты научишься рисовать картины вместе с создателями нейросети Kandinsky 2.1, поставишь спектакль под руководством выпускницы Школы-студии МХАТ, а также запишешь электронный трек, освоишь графический дизайн, создашь NFT и подготовишь портфолио для поступления в творческий вуз. Старт летних кэмпов — 1 июня.

Присоединяйся к обучению в удобном формате: офлайн в Москве или онлайн на платформе СберКласс. Тебя ждет живое общение с преподавателями, командная работа и новые друзья во всех уголках страны.

Подключайся онлайн, получи скидку 20% и участвуй в розыгрыше 12 бесплатных мест в летнем кампусе!

Вчера Гриша Мерзон рассказал замечательное.

Есть теорема «о трех колпаках», замечательная. Теорема эта такая. На плоскости даны три окружности различных радиусов, лежащих снаружи друг-друга. Для каждой пары окружностей из этой тройки проведем внешние касательные, которых тоже две штуки. Эти две касательные пересекутся в точке. Так вот, утверждение теоремы состоит в том, что эти три точки лежат на одной прямой.

Одно из доказательств (вернее идея) таково: надо выйти в пространство — рассмотреть не окружности, а сферы с теми же центрами. Дальше надо положить на эти три сферы плоскость (если это возможно!) пересечение исходной плоскости и положенной плоскости есть нужная прямая.

А вот что рассказал Гриша, пересказывая Бибикова. доказательство (тоже идея) при помощи геометрии Лобачевского.

Оказывается (то есть это простая теорема), две окружности (одна вовне другой) в модели Пуанкаре (на верхней полуплоскости) равны, то есть совмещаются движением если и только если их внешние касательные пересекаются на абсолюте (возможно в бесконечно-удаленной точке)! Тут правильно сказать, что окружности в модели Пуанкаре это обычные евклидовы окружности в верхней полуплоскости (только радиусы их никак не связаны).


В доказательстве главную роль играет то, что гомотетия с центром на абсолюте есть движение плоскости Лобачевского.

Теперь «три колпака» — если есть три окружности, то выберем произвольным образом две разные пары из них (конечно эти пары пересекутся по одной окружности).

Рассмотрим две пары внешних касательных, построенных по выбранным парам окружностей — каждая пара касательных пересечется в какой-то точке (считаем их не бесконечно-удаленными). Проведем через эту пару точек прямую. Назначим ее абсолютом! Тогда окружности из первой и второй пары равны. Значит, равны окружности и из третьей пары, которую мы не рассматривали. Значит, соответствующие внешние касательные тоже пересекаются на абсолюте.

Прекрасное рассуждение, только в нем та же проблема, что и с первым доказательством. Если назначить эту прямую абсолютом, то не верно, вообще говоря, что все три окружности окажутся в одной полуплоскости (которая плоскость Лобачевского). Поэтому, как и в первом доказательстве правильно «выйти в комплексную область». А это почти общематематическая идея.

Оказывается у задачи, предложенной выше, есть очень красивое решение с использованием понятия эквидистанты на плоскости Лобачевского (но все же попробуйте придумать обычное решение). Когда я узнал эту задачу, я тут же выдал ее на московских сборах, но решение с плоскостью Лобачевского рассказать толком так и не смог — запутался, не хватило базовых знаний и опыта 😁. Но в тот момент я подумал, какая же это классная тема — использование всяких штук из плоскости Лобачевского при решении обычных геометрических задач. Подумалось, что таких задач должно со временем становиться все больше и больше. А в 2020-ом году в Мат. Просвещении вышла абсолютно замечательная статья П.В. Бибикова и И.И. Фролова "Неевклидовы решения евклидовых задач."

А теперь самое главное! Через неделю, 6-го мая, в субботу в 18-00 (по московскому времени) у нас на канале состоится онлайн лекция Павла Витальевича Бибикова, в которой будет рассказано о неожиданной связи между евклидовой и неевклидовой геометриями. Оказывается, некоторые простые конструкции из геометрии Лобачевского позволяют быстро решать весьма трудные задачи из геометрии Евклида. Планируется рассказать о нескольких таких задачах, а также попутно немного рассказать о самой геометрии Лобачевского и различных ее моделях. Также будут разобраны несколько классических конструкций: теорема о бабочке, теорема Паскаля, теорема Дезарга об инволюции и теорема Фейербаха.

Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и желательно, но не обязательно представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения).

Доклад скорее всего будет проходить в зуме и, возможно, транслироваться на youtube. Если все пройдет без технических накладок, то запись появится на канале.

Если вы собираетесь присоединиться, то обязательно поставьте 🔥, чтобы я знал ориентировочное количество потенциальных участников.

Собрали папку каналов о математике.
https://tttttt.me/addlist/13qNrj-gNrA4YmJi

Работает так: вы идете по ссылке, видите пачку каналов, выбираете, на какие из них хотите подписаться.

Если мы что-то важное упустили, напишите в комментарии.

о3) Проведем из точки A касательные AX и AY к окружности с центром O. Тогда AX=AY.

э3а) Проведем из точки A касательные AX и AY к эллипсу с центром O. Тогда площади треугольников AXO и AYO равны.

э3б) Проведем из точки A касательные AX и AY к эллипсу с фокусом F. Тогда отрезки AX и AY видны из F под одинаковыми углами.

// Это продолжение серии переходов от окружности к эллипсу (ранее: часть 1, часть 2). Последнее утверждение (за которое спасибо Диме Швецову) предлагается доказать.

Позволю себе задачу, решения которой пока не знаю. В надежде, что кто-то либо решит, либо подскажет, с чем это едят.

Дана некоторая алгебраическая кривая (плоская и гладкая), на ней выбраны три точки A, B и С. Тангенциальным треугольником назовём треугольник DEF, образуемый тремя касательными к кривой в этих точках. Для каких кривых отношение площадей [DEF]/[ABC] равно константе, т.е. не зависит от выбора точек?

В четырехугольнике средняя линия равна полусумме оснований. Доказать, что это трапеция (или параллелограмм).

// Задача, доступная 8 классу, как просили в комментариях.

Дан произвольный четырехугольник. Доказать, что его копиями можно замостить плоскость.

// Предлагается решить эту задачу (она, кстати, была на Московской мат. олимпиаде в 1940 году), а также обдумать связь с предыдущей.
// За сюжет спасибо Н.Стрелковой