Forwarded from Олимпиадная геометрия
Две задачи. Первая с олимпиады ЮМШ для 8-го класса (декабрь 2022, Константин Кноп), а вторая с финала высшей лиги 8-го класса Уральского турнира (май 2023).
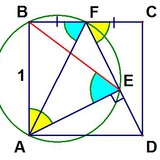
В обоих случаях дан правильный многоугольник и площади трех треугольников. Требуется найти площадь многоугольника.
В обоих случаях дан правильный многоугольник и площади трех треугольников. Требуется найти площадь многоугольника.
👍17❤2😢2
Геометрия-канал
Дан произвольный четырехугольник. Доказать, что его копиями можно замостить плоскость. // Предлагается решить эту задачу (она, кстати, была на Московской мат. олимпиаде в 1940 году), а также обдумать связь с предыдущей. // За сюжет спасибо Н.Стрелковой
про замощение плоскости произвольными четырехугольниками и его применение к решению геометрических задач можно почитать в статье Болтянского «Паркет из четырехугольников» в Кванте
http://kvant.mccme.ru/1989/11/parket_iz_chetyrehugolnikov.htm
http://kvant.mccme.ru/1989/11/parket_iz_chetyrehugolnikov.htm
👍11❤2🔥1
Forwarded from Непрерывное математическое образование
https://www.mathnet.ru/rus/kvant1726
напомним и статью В.Н.Дубровского «Геометрия на паркете»
там при помощи подходящих замощений плоскости доказывается теорема Пифагора, теорема Наполеона и проч.
напомним и статью В.Н.Дубровского «Геометрия на паркете»
там при помощи подходящих замощений плоскости доказывается теорема Пифагора, теорема Наполеона и проч.
👍12
Forwarded from Непрерывное математическое образование
https://cs.uwaterloo.ca/~csk/spectre/
если в предыдущем примере¹ апериодического замощения одной плиткой вас смущала необходимость перевораичвать часть плиток, то есть хорошие новости
«we … produce a family of shapes we call “Spectres”, which are strictly chiral aperiodic monotiles: they tile aperiodically using only translations and rotations, even when reflections are permitted»
¹ https://xn--r1a.website/cme_channel/3154
если в предыдущем примере¹ апериодического замощения одной плиткой вас смущала необходимость перевораичвать часть плиток, то есть хорошие новости
«we … produce a family of shapes we call “Spectres”, which are strictly chiral aperiodic monotiles: they tile aperiodically using only translations and rotations, even when reflections are permitted»
¹ https://xn--r1a.website/cme_channel/3154
❤9👍3
Forwarded from И так далее — математика
Летние интенсивы по геометрии 🔥
Геометрия – одна из самых красивых и наглядных сфер олимпиадной математики. Ей можно заниматься бесконечно долго, и всё равно останется то, чего вы ещё не знаете.
Кому-то геометрия очень нравится, у кого-то наоборот она совсем не получается. Верно одно – практически никого геометрия не оставляет равнодушным!
Видели много запросов на интенсив именно по геометрии, и постарались сделать самое лучшее, что могли.
И, кажется, у нас получилось)
Итак, объявляем интенсивы по геометрии от Фёдора Львовича Бахарева:
⭐️ Создателя канала "Олимпиадная геометрия» – @olympgeom
⭐️ Кандидата физико-математических наук, старшего научного сотрудника лаборатории им. П.Л. Чебышева
⭐️ Автора множества задач по олимпиадой геометрии
Сами занятия будут совмещать в себе лекции и семинары - так участники смогут узнать новые и свежо взглянуть на уже пройденные ранее темы, а также применить свои знания на практике.
Вести лекции, разборы и составлять программу будет непосредственно Фёдор Львович. На проведение семинаров и отслушивание задач позовём молодых преподавателей с высокими олимпиадными достижениями, чтобы они могли поделиться своим опытом и любовью к геометрии с участниками.
7 класс
Даты – 30 июля - 6 августа.
Занятия каждый день с 12:15 до 15:15
Смена отлично подойдёт ребятам, желающим хорошо решать задачи уровня региона-закла Эйлера или Уральского турнира в следующем учебном году.
8-9 класс
Даты – 22-29 июля.
Занятия каждый день с 12:15 до 15:15
Смена отлично подойдёт ребятам, желающим хорошо решать задачи уровня региона-закла Всеросса в следующем учебном году.
Подробную информацию о методической составляющей смен можете найти в приложенных фотографиях. На обеих сменах будем рады видеть участников, имеющих минимальные необходимые знания и желающих позаниматься геометрией.
Стоимость участия в одной смене – 19500
Ссылка на регистрацию – https://forms.gle/8jfj9NJGekgGfTFT8
Геометрия – одна из самых красивых и наглядных сфер олимпиадной математики. Ей можно заниматься бесконечно долго, и всё равно останется то, чего вы ещё не знаете.
Кому-то геометрия очень нравится, у кого-то наоборот она совсем не получается. Верно одно – практически никого геометрия не оставляет равнодушным!
Видели много запросов на интенсив именно по геометрии, и постарались сделать самое лучшее, что могли.
И, кажется, у нас получилось)
Итак, объявляем интенсивы по геометрии от Фёдора Львовича Бахарева:
⭐️ Создателя канала "Олимпиадная геометрия» – @olympgeom
⭐️ Кандидата физико-математических наук, старшего научного сотрудника лаборатории им. П.Л. Чебышева
⭐️ Автора множества задач по олимпиадой геометрии
Сами занятия будут совмещать в себе лекции и семинары - так участники смогут узнать новые и свежо взглянуть на уже пройденные ранее темы, а также применить свои знания на практике.
Вести лекции, разборы и составлять программу будет непосредственно Фёдор Львович. На проведение семинаров и отслушивание задач позовём молодых преподавателей с высокими олимпиадными достижениями, чтобы они могли поделиться своим опытом и любовью к геометрии с участниками.
7 класс
Даты – 30 июля - 6 августа.
Занятия каждый день с 12:15 до 15:15
Смена отлично подойдёт ребятам, желающим хорошо решать задачи уровня региона-закла Эйлера или Уральского турнира в следующем учебном году.
8-9 класс
Даты – 22-29 июля.
Занятия каждый день с 12:15 до 15:15
Смена отлично подойдёт ребятам, желающим хорошо решать задачи уровня региона-закла Всеросса в следующем учебном году.
Подробную информацию о методической составляющей смен можете найти в приложенных фотографиях. На обеих сменах будем рады видеть участников, имеющих минимальные необходимые знания и желающих позаниматься геометрией.
Стоимость участия в одной смене – 19500
Ссылка на регистрацию – https://forms.gle/8jfj9NJGekgGfTFT8
Please open Telegram to view this post
VIEW IN TELEGRAM
Please open Telegram to view this post
VIEW IN TELEGRAM
❤8🤩8👍4🔥4😢2
Непрерывное математическое образование
https://geometry.ru/olimp/2023/zaoch_2023.pdf https://geometry.ru/olimp/2023/zaoch_eng_2023.pdf начинается заочный тур XIX олимпиады им. И.Ф.Шарыгина 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
опубликованы решения заочного тура олимпиады Шарыгина этого года:
https://geometry.ru/olimp/2023/zaoch_sol_2023.pdf
а также информация о финале в конце июля (в т.ч. списки приглашенных туда): https://geometry.ru/olimp/2023.php#final
https://geometry.ru/olimp/2023/zaoch_sol_2023.pdf
а также информация о финале в конце июля (в т.ч. списки приглашенных туда): https://geometry.ru/olimp/2023.php#final
👍12😱3🎉1
Forwarded from Быстрые задачки по математике (Alexey Sgibnev)
Отрезок AB пересекает прямую k (см. рис.). На прямой k отметили точку C, так что треугольник ABC — равнобедренный. Сколько таких точек C существует?
Anonymous Quiz
23%
1
21%
2
21%
3
11%
4
25%
5
👍11🔥1
А вот Константин Кноп продолжает тему предыдущей задачи:
На плоскости даны три точки A, B, C, являющиеся вершинами неравнобедренного треугольника. Сколько может существовать (тоже в плоскости, разумеется!) таких точек D, для которых хотя бы два из треугольников ABD, ACD, BCD — равнобедренные?
Интересуют все варианты ответа, а не только один «самый произвольный случай».
Источник: https://www.facebook.com/groups/mathpuz/permalink/2502301789945648/?mibextid=Nif5oz
На плоскости даны три точки A, B, C, являющиеся вершинами неравнобедренного треугольника. Сколько может существовать (тоже в плоскости, разумеется!) таких точек D, для которых хотя бы два из треугольников ABD, ACD, BCD — равнобедренные?
Интересуют все варианты ответа, а не только один «самый произвольный случай».
Источник: https://www.facebook.com/groups/mathpuz/permalink/2502301789945648/?mibextid=Nif5oz
👍10👎3
В треугольнике ABC провели биссектрисы AA', BB', CC'. Известно, что ∠ABC=120°. Найти ∠A'B'C'.
// Задача М.Шебаршина, не очень простая, но ничего сверх программы 7 класса знать не обязательно.
// Задача М.Шебаршина, не очень простая, но ничего сверх программы 7 класса знать не обязательно.
❤19👍3🔥1🎉1
Пару лет назад мы с коллегами (Наталья Нетрусова, Алексей Сгибнев, Антон Сысоев) сделали курс «Геогебра для учителей»: семь видеоуроков + практические задания. В тот момент он был открыт для учителей Матвертикали, мы проверяли задания и писали к ним замечания. Сейчас мы решили выложить этот курс в свободный доступ, но только без проверки: каждый желающий практикуется на заготовках и сам себя проверяет.
Курс сделан в виде GeoGebraBook и доступен даже без регистрации в Геогебре:
https://www.geogebra.org/m/jdg8nz9e
Курс сделан в виде GeoGebraBook и доступен даже без регистрации в Геогебре:
https://www.geogebra.org/m/jdg8nz9e
❤30👍11🔥3🎉2🤩1
Forwarded from Pavel K
Доказать, что периметр любого остроугольного треугольника по крайней мере вдвое больше диаметра описанной около него окружности.
🤔12❤6👍3
самое прямолинейное решение задачи https://xn--r1a.website/geometrykanal/2141 — посмотреть на две пары подобных треугольников и выразить отрезки LB и BR; их равенство — это в точности условие теоремы Чевы
но можно и совсем без вычислений: нам нужнодоказать, что четверка проходящих через B' прямых гармоническая — а в такой форме это утверждение проективно-инвариантное, поэтому достаточно решить задачу для случая, когда чевианы суть медианы
в качестве бонуса предлагается вывести из этой задачи
1) что высоты треугольника являются биссектрисами ортотреугольника;
2) обратное утверждение к задаче Шебаршина https://xn--r1a.website/geometrykanal/2140
но можно и совсем без вычислений: нам нужно
в качестве бонуса предлагается вывести из этой задачи
1) что высоты треугольника являются биссектрисами ортотреугольника;
2) обратное утверждение к задаче Шебаршина https://xn--r1a.website/geometrykanal/2140
👍11❤1
Forwarded from Олимпиадная геометрия
Очень классная задача с ELMO-2023 (Problem 3). С очень содержательным теоретическим материалом, скрывающимся за конструкцией.
Три подобных четырехугольника расположены так, как показано на рисунке. Докажите, что их точки пересечения диагоналей лежат на одной прямой.
Три подобных четырехугольника расположены так, как показано на рисунке. Докажите, что их точки пересечения диагоналей лежат на одной прямой.
❤13👍2😱2🤔1
Forwarded from Быстрые задачки по математике (Alexey Sgibnev)
Две неравные стороны одного равнобедренного треугольника равны двум сторонам другого равнобедренного треугольника. Верно ли, что треугольники равны?
Anonymous Quiz
34%
Да
66%
Нет
🔥18😢14🥱8🎉2😁1
Верно ли, что любой прямоугольный треугольник можно с помощью циркуля и линейки разделить на два меньших так, что в меньших треугольниках найдётся по равной биссектрисе?
(Доступная задача Шаповалова с закончившегося недавно турнира Савина.)
(Доступная задача Шаповалова с закончившегося недавно турнира Савина.)
🔥13👍5👎1
IMG_20230709_082302_056.png
116.8 KB
Федор Львович прямо сейчас в зуме рассказывает, что наш канал — это канал слишком простых геометрических задач.
Мне кажется, это не баг, а фича. Вот еще одна
Мне кажется, это не баг, а фича. Вот еще одна
❤21😁3👍1