Всем привет!

Итак, в ближайшую пятницу, 3-го марта, в 20-00 по московскому времени состоится стрим "Как доказывать перпендикулярность?" Мы будем в основном разбирать задачи, продвигаясь от более простых методов к более сложным. Некоторые задачи будут, конечно, разобраны по нескольку раз с примененим разных методов. Список задач пока окончательно не сформирован, поэтому его не выкладываю.

Итак, сегодня, 5-го марта, в 20-00 по московскому времени я буду прорешивать в режиме онлайн задачи заочного тура олимпиады Шарыгина. Спасибо всем за заинтересованность в этом меропритии. ссылка на стрим ниже.

https://youtube.com/live/jeBg7zL1jTQ?feature=share

Эллипс c фокусами в серединах сторон AB и AC треугольника ABC проходит через вершину A, а эллипс c фокусами в серединах сторон AC и BC проходит через вершину C.

Докажите, что точки пересечения этих эллипсов и ортоцентр треугольника ABC лежат на одной прямой.

===

Это задача А.Марданова с заочного тура олимпиады Шарыгина. Предлагается получить это утверждение практически бесплатно из https://tttttt.me/geometrykanal/1981 (via «Олимпиадная геометрия» и комментарии автора там)

Докажите, что в прямоугольном треугольнике с углом 30 градусов одна биссектриса в два раза короче другой.

(задача от Егора Бакаева на ММО вчера)

в комментариях к предыдущей задаче есть уже штук 5 разных решений. а вот такое неожиданное решение хочется вынести и в канал:

Достроим данный треугольник до правильного 12-угольника. Тогда все линии проходят по диагоналям этого 12-угольника: d_4 - диагональ через 4 стороны, d_5 - через 5 сторон, d_6 - через 6 сторон. Зелёный отрезок - средняя линия в треугольнике, в силу зеркальной симметрии относительно содержащей его диагонали. Значит, он делит биссектрису пополам, а половина этой биссектрисы - часть d_5 до пересечения с d_6 - равна второй биссектрисе.

На сторонах равностороннего треугольника построены во внешнюю сторону треугольники так, что отмеченные стороны равны, а углы A, B, C шестиугольника больше 120 градусов. Докажите, что из красного, зеленого и синего отрезков можно составить треугольник.

(задача Д.Бродского с ММО-2023)

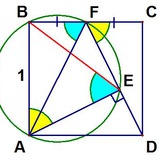
Красные отрезки равны. Синие отрезки равны. Докажите, что три точки, которые как будто бы лежат на пунктирной прямой — действительно лежат на одной прямой.

(Понравилась задача из «Олимпиадной геометрии» — но там плохо понял обсуждение, а может здесь кто-то объяснит прямо, как решать?)

https://arxiv.org/abs/2303.10798
https://cs.uwaterloo.ca/~csk/hat/

D.Smith, J.S.Myers, C.S.Kaplan, C.Goodman-Strauss пишут, что нашли одну плитку, которой можно замостить плоскость, но только апериодически

#реклама
🔥Обучаться востребованной профессии и работать по специальности сразу после 9 класса – реально?

Образовательный центр «Алабуга Политех» по подготовке квалифицированных рабочих кадров предоставляет возможность не только освоить специальность будущего бесплатно, но и начать зарабатывать до 77 тысяч рублей с первого курса!

Учеба будет проходить на территории крупнейшей в России особой экономической зоны «АЛАБУГА».

Какие еще плюсы учебы в Алабуга Политех?

✅13 востребованных направлений: механика и робототехника, программирование Python, BIM-проектирование, сестринское дело и другие;

✅Поступление без экзаменов;

✅100% гарантия трудоустройства во время и после обучения;

✅Проживание для иногородних студентов.

Подать заявку на поступление можно уже сейчас: нужно пройти быструю регистрацию на сайте Алабуга Политех. Количество мест ограничено 🚀

Много окружностей не бывает! Это мог бы быть лозунг к конкурсу №3, который подойдет к концу приблизительно через неделю! Напоминаю, что я очень жду ваших работ!

Но на самом деле это лозунг к прекрасной задаче девятиклассника Ильи Замоторина, которая попала под номером 6 в вариант 10-11 класса открытой олимпиады 239, прошедшей не прошлых выходных.

Симметрическая разность двух гомотетичных треугольников T1 и T2 состоит из шести треугольников t1,...,t6 с описанными окружностями ω1, ω2,... ,ω6 (подряд против часовой стрелки, никакие две не пересекаются). Окружность Ω1 с центром O1 касается ω1, ω3 и ω5 внешним образом; окружность Ω2 с центром O2 касается ω2, ω4 и ω6 внешним образом; окружность Ω3 с центром O3 касается ω1, ω3 и ω5 внутренним образом; окружность Ω4 с центром O4 касается ω2, ω4 и ω6 внутренним образом.
Докажите, что O1O3 = O2O4.

доказать, что ортоцентр H, середина стороны M и точка пересечения внутренних касательных X лежат на одной прямой

(задача И.Михайлова со второго дня 11 класса ММО-2023)

в комментариях у «Олимпиадной геометрии» Давид Ванеев предложил такое обобщение предыдущей задачи

доказать, что для любого вписанного четырехугольника точка пересечения диагоналей H, центр окружности M и точка пересечения общих внутренних касательных X лежат на одной прямой

(предыдущая задача получается, если M лежит на стороне четырехугольника)

upd: более того, красная и синяя окружности могут и не касаться сторон четырехугольника, достаточно того, что они вписаны в углы

#реклама

🤔 А ты знал, что участник списка Forbes Бен Пастернак уже в 17 лет разработал свое первое приложение Impossible Rush, потому что ему было скучно сидеть на уроках в школе? Оно обошло Tinder и Twitter, заняв 16-е место в чартах App Store. Потом парень разработал, сетевую платформу для видеочата Monkey, которая позже была приобретена компанией Holla, и SIMULATE, компанию по устойчивому питанию, стоимость которой сегодня превышает $250 млн.

Если ты молодой начинающий предприниматель, который думает о развитии собственного дела, подписывайся на канал Юнби.

💥 Тут ты найдешь лайфхаки и советы на тему старта собственного проекта, узнаешь новости из мира бизнеса и поднимешь себе настроение веселыми видео про начинающих предпринимателей.

Wild Mathing рассказывает про разные геометрические свойства параболы:

https://youtu.be/gRb-qD_lm8w

( в частности, рекламирует задачу https://tttttt.me/geometrykanal/2041 )

Точку на описанной окружности треугольника отразили относительно его стороны BC и получили точку M₁. Доказать, что окружность, проходящая через середины сторон треугольника, делит AM₁ пополам.

(Задача Д.Мухина на устной олимпиаде по геометрии сегодня.)