Forwarded from Pavel Kalugin
Простенькая и, как мне кажется, красивая задача:
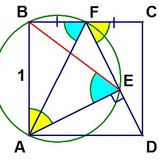
ABCD — прямоугольник, M — середина AB. Перпендикуляр из A на DM вторично пересекает описанную около прямоугольника окружность в точке F.
Доказать, что DM делит AF в отношении 1:2.
ABCD — прямоугольник, M — середина AB. Перпендикуляр из A на DM вторично пересекает описанную около прямоугольника окружность в точке F.
Доказать, что DM делит AF в отношении 1:2.
#реклама
Про программирование и обучение в сфере IT
Школа программистов МШП набирает детей: очное и онлайн обучение с углублённой программой.
С 3-го по 11-й классы!
Ученики и выпускники школы сдают ЕГЭ на высокие баллы, выигрывают олимпиады, поступают в лучшие вузы (МГУ, МФТИ, ВШЭ, «Бауманка» и другие) и находят работу в ВК, Яндексе и других крупных компаниях. Для учеников Школы есть спецкурсы по подготовке к ОГЭ и ЕГЭ по математике и информатике.
Все подробности можно узнать на сайте https://online.informatics.ru. Важно: оплатить обучение можно средствами маткапитала!
И промокод info2022 даёт скидку 15% на первый месяц обучения в Онлайн-отделении школы.
Для жителей Москвы, МО и Санкт-Петербурга доступно очное обучение:
Москва — https://mshp.informatics.ru
Санкт-Петербург — https://spb.informatics.ru
Про программирование и обучение в сфере IT
Школа программистов МШП набирает детей: очное и онлайн обучение с углублённой программой.
С 3-го по 11-й классы!
Ученики и выпускники школы сдают ЕГЭ на высокие баллы, выигрывают олимпиады, поступают в лучшие вузы (МГУ, МФТИ, ВШЭ, «Бауманка» и другие) и находят работу в ВК, Яндексе и других крупных компаниях. Для учеников Школы есть спецкурсы по подготовке к ОГЭ и ЕГЭ по математике и информатике.
Все подробности можно узнать на сайте https://online.informatics.ru. Важно: оплатить обучение можно средствами маткапитала!
И промокод info2022 даёт скидку 15% на первый месяц обучения в Онлайн-отделении школы.
Для жителей Москвы, МО и Санкт-Петербурга доступно очное обучение:
Москва — https://mshp.informatics.ru
Санкт-Петербург — https://spb.informatics.ru
В треугольнике ABC точки D, E и F выбраны на сторонах BC, CA и AB соответственно так, что AD, BE и CF пересекаются в одной точке. Окружности (AFE) и (CDE) пересекаются в точке T. Докажите, что окружности (ATD), (BTE), (CTF) имеют общую радикальную ось.
(задача П.Пучкова и Е.Сапожникова с Южного турнира, via И.Кухарчук@vk)
(задача П.Пучкова и Е.Сапожникова с Южного турнира, via И.Кухарчук@vk)
Forwarded from Непрерывное математическое образование
наверное все здесь знают базу задач по математике problems.ru (а некоторые — и zadachi.mccme.ru)
а вот сегодня открылась база лингвистических задач, http://lingproblems.online/
«Здесь собраны задачи, предлагавшиеся на различных олимпиадах по лингвистике с 1965 года. В настоящий момент в базу включены задачи, предлагавшиеся на Московской традиционной олимпиаде по лингвистике, Турнире имени М. В. Ломоносова, Международной олимпиаде по лингвистике, олимпиаде «Высшая проба» по русскому языку, олимпиаде Образовательного центра «Сириус» и Пригласительной олимпиаде по лингвистике, а также опубликованные в некоторых сборниках. Задачи снабжены указателем по авторам и языкам. Приятного Вам решения!»
а вот сегодня открылась база лингвистических задач, http://lingproblems.online/
«Здесь собраны задачи, предлагавшиеся на различных олимпиадах по лингвистике с 1965 года. В настоящий момент в базу включены задачи, предлагавшиеся на Московской традиционной олимпиаде по лингвистике, Турнире имени М. В. Ломоносова, Международной олимпиаде по лингвистике, олимпиаде «Высшая проба» по русскому языку, олимпиаде Образовательного центра «Сириус» и Пригласительной олимпиаде по лингвистике, а также опубликованные в некоторых сборниках. Задачи снабжены указателем по авторам и языкам. Приятного Вам решения!»
#реклама
🍁 Олимпиадный сезон уже начался. Время прокачать свои навыки вместе с Олимпиадными школами МФТИ.
Открыта регистрация на осенние смены в двух форматах: дистанционном с 29 октября по 5 ноября и впервые осенью — на территории кампуса МФТИ с 29 октября по 6 ноября.
Направления очной смены:
🔢математика (9–11 класс);
⚛️ физика (7–8 класс);
🦠 биология (9–11 класс).
Направления онлайн-смены:
🔢 математика (5–11 класс);
⚛️ физика (9–11 класс);
💻 информатика (6–11 класс);
🧪 химия (8–11 класс).
Учеников ожидают:
✅Интенсивная 36-часовая программа по одной из выбранных дисциплин на выбор: математика, физика, химия, информатика и биология.
✅Подготовка к отличному выступлению на всех этапах ВсОШ и олимпиад из перечня РСОШ.
✅Разбор домашних заданий и персональные консультации с ассистентами преподавателей (3-4 часа ежедневно).
✅Множество творческих мастер-классов, научно-популярных лекций и развлекательных мероприятий.
✅5-ти разовое питание и проживание на территории кампуса МФТИ — при участии в очном формате.
✅Самая выгодная стоимость — при участии в онлайн формате.
Регистрируйтесь и узнавайте подробнее об Олимпиадных школах МФТИ, расписании и преподавателях: https://it-edu.com/xe6a
🍁 Олимпиадный сезон уже начался. Время прокачать свои навыки вместе с Олимпиадными школами МФТИ.
Открыта регистрация на осенние смены в двух форматах: дистанционном с 29 октября по 5 ноября и впервые осенью — на территории кампуса МФТИ с 29 октября по 6 ноября.
Направления очной смены:
🔢математика (9–11 класс);
⚛️ физика (7–8 класс);
🦠 биология (9–11 класс).
Направления онлайн-смены:
🔢 математика (5–11 класс);
⚛️ физика (9–11 класс);
💻 информатика (6–11 класс);
🧪 химия (8–11 класс).
Учеников ожидают:
✅Интенсивная 36-часовая программа по одной из выбранных дисциплин на выбор: математика, физика, химия, информатика и биология.
✅Подготовка к отличному выступлению на всех этапах ВсОШ и олимпиад из перечня РСОШ.
✅Разбор домашних заданий и персональные консультации с ассистентами преподавателей (3-4 часа ежедневно).
✅Множество творческих мастер-классов, научно-популярных лекций и развлекательных мероприятий.
✅5-ти разовое питание и проживание на территории кампуса МФТИ — при участии в очном формате.
✅Самая выгодная стоимость — при участии в онлайн формате.
Регистрируйтесь и узнавайте подробнее об Олимпиадных школах МФТИ, расписании и преподавателях: https://it-edu.com/xe6a
Одна окружность пересекает параболу точка A,B,C,D. Вторая окружность — в точках A,B,E,F. Докажите, что CD||EF.
// Задача с сегодняшнего конкурса учителей. Можно решить, а также подумать про обобщения и т.п.
// Задача с сегодняшнего конкурса учителей. Можно решить, а также подумать про обобщения и т.п.
Forwarded from Непрерывное математическое образование
http://mi.mathnet.ru/kvant342
в продолжение темы — статья П.Кожевникова «Антипараллели и коники» в Кванте №8 за 2017 год
в продолжение темы — статья П.Кожевникова «Антипараллели и коники» в Кванте №8 за 2017 год
в обсуждениях — К.Кноп рассказывает разное интересное вокруг https://en.wikipedia.org/wiki/Langley%27s_Adventitious_Angles — см https://tttttt.me/c/1141607031/27776 и далее
Wikipedia
Langley's Adventitious Angles
Geometry puzzle
#реклама
Участвуйте в Национальной олимпиаде по анализу данных DANO для школьников 9–11 классов.
НИУ ВШЭ и Тинькофф открывают набор на всероссийский проект для ребят, которые хотят стать аналитиками. Вас ждут реальные задачи, полезные материалы от экспертов в области анализа данных и, конечно, призы и подарки.
Зачем участвовать?
— Возможность получить дополнительные баллы при поступлении в вузы-соорганизаторы;
— шанс поступить в НИУ ВШЭ на места за счет средств университета;
— бесценный опыт работы в команде во время выезда на неделю в Подмосковье;
— бесплатное обучение: перед каждым этапом олимпиады будет образовательный блок.
Зарегистрируйтесь до 3 октября: https://v.tinkoff.ru/danocontest.ru
Участвуйте в Национальной олимпиаде по анализу данных DANO для школьников 9–11 классов.
НИУ ВШЭ и Тинькофф открывают набор на всероссийский проект для ребят, которые хотят стать аналитиками. Вас ждут реальные задачи, полезные материалы от экспертов в области анализа данных и, конечно, призы и подарки.
Зачем участвовать?
— Возможность получить дополнительные баллы при поступлении в вузы-соорганизаторы;
— шанс поступить в НИУ ВШЭ на места за счет средств университета;
— бесценный опыт работы в команде во время выезда на неделю в Подмосковье;
— бесплатное обучение: перед каждым этапом олимпиады будет образовательный блок.
Зарегистрируйтесь до 3 октября: https://v.tinkoff.ru/danocontest.ru
Геометрия-канал
Одна окружность пересекает параболу точка A,B,C,D. Вторая окружность — в точках A,B,E,F. Докажите, что CD||EF. // Задача с сегодняшнего конкурса учителей. Можно решить, а также подумать про обобщения и т.п.
Две параболы с перпендикулярными осями пересекаются по 4 точкам. Доказать, что эти точки лежат на одной окружности.
(Это довольно близко к обсуждавшейся недавно задаче с конкурса учителей.)
(Это довольно близко к обсуждавшейся недавно задаче с конкурса учителей.)
Имеются два софокусных эллипса. Из двух точек на одном проводят касательные к другому. Доказать, что возникающий четырехугольник описанный, а две его другие вершины лежат на гиперболе с теми же фокусами.
(Из коллекции «Fun Problems in Geometry and Beyond», собранной С.Л.Табачниковым и Б.А.Хесиным в честь 80-летия Д.Б.Фукса.)
(Из коллекции «Fun Problems in Geometry and Beyond», собранной С.Л.Табачниковым и Б.А.Хесиным в честь 80-летия Д.Б.Фукса.)
#реклама
📖 Математика для взрослых!
На просторах телеграма появился классный бот-тренажер, где собрано множество задач, тестов и видеоуроков по математике!
Этот бот создан для того, чтобы с помощью математики👇
- развивать вашу эрудицию;
- научиться познавать мир при помощи упрощения сложных ментальных объектов;
- используя абстракции, развивать логику;
- тренировать вдумчивость и навык «правильного сомнения»
📚Весь материал подготовлен доктором философских наук, математиком, логиком и основателем одного из крупнейших онлайн-сообществ по математике. Материал включает в себя более 50 заданий с тестами и задачами!
👉Переходите в бот и начинайте занятия уже сегодня: clck.ru/32JipX
📖 Математика для взрослых!
На просторах телеграма появился классный бот-тренажер, где собрано множество задач, тестов и видеоуроков по математике!
Этот бот создан для того, чтобы с помощью математики👇
- развивать вашу эрудицию;
- научиться познавать мир при помощи упрощения сложных ментальных объектов;
- используя абстракции, развивать логику;
- тренировать вдумчивость и навык «правильного сомнения»
📚Весь материал подготовлен доктором философских наук, математиком, логиком и основателем одного из крупнейших онлайн-сообществ по математике. Материал включает в себя более 50 заданий с тестами и задачами!
👉Переходите в бот и начинайте занятия уже сегодня: clck.ru/32JipX
#реклама
Приглашаем детей 10–13 лет прокачать математику через игру!
Это обучающая игра для развития Math skills, темы разработаны русскими преподавателями математики с большим опытом, а задачи специально созданы с учетом возраста детей и постепенного усложнения уровня.
Детей ждут задачи из теории графов, логики, криптографии, комбинаторики и теории чисел; стратегии для одного игрока и для команд; квесты и задания, HelpBot и чаты для общения — все, что нужно для освоения мира, где всем заправляет искусственный интеллект.
• Игру можно проходить на русском или английском языке.
• Участие 65$ в месяц, а дети из Украины — играют бесплатно.
• Первый пробный месяц игры — бесплатно для всех.
• Главный приз — поездка в умный лагерь «Марабу»!
ВПЕРЕД! В игру! https://bit.ly/3Txnv2U
Приглашаем детей 10–13 лет прокачать математику через игру!
Это обучающая игра для развития Math skills, темы разработаны русскими преподавателями математики с большим опытом, а задачи специально созданы с учетом возраста детей и постепенного усложнения уровня.
Детей ждут задачи из теории графов, логики, криптографии, комбинаторики и теории чисел; стратегии для одного игрока и для команд; квесты и задания, HelpBot и чаты для общения — все, что нужно для освоения мира, где всем заправляет искусственный интеллект.
• Игру можно проходить на русском или английском языке.
• Участие 65$ в месяц, а дети из Украины — играют бесплатно.
• Первый пробный месяц игры — бесплатно для всех.
• Главный приз — поездка в умный лагерь «Марабу»!
ВПЕРЕД! В игру! https://bit.ly/3Txnv2U
Forwarded from Олимпиадная геометрия
Czech-Polish-Slovak match-2022, Problem 5.
Точка O — центр описанной окружности треугольника ABC, в котором AB < AC. Точка Y — середина биссектрисы AD угла A. Перпендикуляр в точке D к прямой BC пересекает AO в точке X. Докажите, что точки B, C, X и Y лежат на одной окружности.
Точка O — центр описанной окружности треугольника ABC, в котором AB < AC. Точка Y — середина биссектрисы AD угла A. Перпендикуляр в точке D к прямой BC пересекает AO в точке X. Докажите, что точки B, C, X и Y лежат на одной окружности.