Forwarded from Даша Иванова
Сняла мультфильм про математику велосипедных следов на конкурс SoME2 – хочу поделиться!
https://youtu.be/l7bYY2U5ld8
https://youtu.be/l7bYY2U5ld8
YouTube
A Curious Track, or What Bikes Are Hiding From Us
Sources:
George Hart for The Simons Foundation, Bicycle Tracks - Which Way Did the Bicycle Go? https://www.youtube.com/watch?v=ETnbfZUW8zY
David Finn, Can a bicycle create a unicycle track. https://www.maa.org/sites/default/files/pdf/upload_library/22/Polya/Finn.pdf…
George Hart for The Simons Foundation, Bicycle Tracks - Which Way Did the Bicycle Go? https://www.youtube.com/watch?v=ETnbfZUW8zY
David Finn, Can a bicycle create a unicycle track. https://www.maa.org/sites/default/files/pdf/upload_library/22/Polya/Finn.pdf…
видео с доказательством теоремы о семи окружностях при помощи гиперболической геометрии: https://youtu.be/m9v0h2ibYpo
( ранее на тему теоремы о семи окружностях: https://tttttt.me/geometrykanal/1920 )
( ранее на тему теоремы о семи окружностях: https://tttttt.me/geometrykanal/1920 )
YouTube
The Seven Circles Theorem
This video is based on a paper by Drach and Schwartz.
Drach, K., Schwartz, R.E. A Hyperbolic View of the Seven Circles Theorem.
Math Intelligencer 42, 61–65 (2020). https://doi.org/10.1007/s00283-019-09952-1
You can read a preprint of the paper here:
h…
Drach, K., Schwartz, R.E. A Hyperbolic View of the Seven Circles Theorem.
Math Intelligencer 42, 61–65 (2020). https://doi.org/10.1007/s00283-019-09952-1
You can read a preprint of the paper here:
h…
This media is not supported in your browser
VIEW IN TELEGRAM
Куб вращается вокруг диагонали (в гиперболоиде).
Вы располагаете пластинкой, имеющей форму правильного треугольника со стороной а и высотой h. Пользуясь только этой пластинкой (и карандашом), требуется:
а) провести через данную точку А параллель к данной прямой l;
б) построить середину данного отрезка AB;
в) провести через данную точку А перпендикуляр к данной прямой l;
г) построить отрезок, соединяющий две данные точки А и В, расстояние между которыми больше а.
источник: https://www.mathedu.ru/text/mp_1958_v3/p270/
а) провести через данную точку А параллель к данной прямой l;
б) построить середину данного отрезка AB;
в) провести через данную точку А перпендикуляр к данной прямой l;
г) построить отрезок, соединяющий две данные точки А и В, расстояние между которыми больше а.
источник: https://www.mathedu.ru/text/mp_1958_v3/p270/
Библиотека Mathedu.Ru
Математическое просвещение. Вып. 3. — 1958 // Библиотека Mathedu.Ru
Математическое просвещение : математика, ее преподавание, приложения и история / под ред. Я. С. Дубнова, А. А. Ляпунова, А. И. Маркушевича. — М. : Физмагиз, 1958. — Вып. 3. — 320 с., 1 л. вкл.
Геометрия-канал
Куб вращается вокруг диагонали (в гиперболоиде).
Оказалось, что на «Математических этюдах» такая модель тоже есть: https://etudes.ru/models/cube-rotation/
etudes.ru
Вращающийся куб / Модели // Математические этюды
Вращающийся вокруг диагонали рёберный куб может служить и артобъектом, и источником задач для размышления.
на боковых сторонах произвольного треугольника построили по правильному — найти углы закрашенного треугольника с вершинами в серединах сторон (via А.Щетников)
в «Квантике» №8 за 2020 год была статья Егора Бакаева про квадраты
https://old.kvantik.com/art/files/pdf/2020-08.10-15.pdf
там можно найти много задач и решений — в частности, простое доказательство упоминавшейся вчера теоремы ван Обеля
https://old.kvantik.com/art/files/pdf/2020-08.10-15.pdf
там можно найти много задач и решений — в частности, простое доказательство упоминавшейся вчера теоремы ван Обеля
Forwarded from Авва
Очередная прекрасная задачка от Катрионы Агг (Ширер). Найти площадь прямоугольника.
(в комментариях могут быть спойлеры)
(может показаться сложной, но уверяю, что задача берется. Никаких эзотерических знаний или приемов не нужно. Верьте в себя и не сдавайтесь)
(в комментариях могут быть спойлеры)
(может показаться сложной, но уверяю, что задача берется. Никаких эзотерических знаний или приемов не нужно. Верьте в себя и не сдавайтесь)
https://youtu.be/86wriGm7i4g
Андрей Щетников доказывает теорему о вписанном угле
даже если знаете стандартное доказательство, мб заинтересует вторая половина — с движениями вместо разбора случаев
Андрей Щетников доказывает теорему о вписанном угле
даже если знаете стандартное доказательство, мб заинтересует вторая половина — с движениями вместо разбора случаев
YouTube
Вписанные углы в окружности
Доказываем теорему о том, что вписанные углы, опирающиеся на одну дугу, равны между собой. Делаем это двумя способами: через центральный угол и через поворот и параллельный перенос.
Доказать, что если окружности, вписанные в два треугольника, на которые разбивается некоторый четырехугольник одной из своих диагоналей, касаются, то будут касаться и окружности, вписанные в треугольники, на которые разбивается этот же четырехугольник второй диагональю.
(еще несложная задача — продолжаю читать 2-ю серию МатПросвещения)
(еще несложная задача — продолжаю читать 2-ю серию МатПросвещения)
Forwarded from Théo D'or
А вот тут обсуждается это неравенство и задача с IMO-1996 с очень похожими мотивами. А еще есть очень красивое усиление неравенства Эрдеша-Морделла — расстояния до вершин можно заменить можно заменить на расстояния до касательных к описанной окружности. И это неравенство доказывается вроде бы проще исходного. https://vk.com/@olympgeom-imo-1996-problem-5-reshenie
VK
IMO-1996, problem 5, решение
Всем привет! Сегодня разбираем действительно сложную задачу с IMO-1996. Задачу, которую не решил ни один российский участник, а сборная К..
Forwarded from tropical saint petersburg
в 1839 году синтетические итальянские геометры (Винченсо Флаути) предложили аналитическим геометрам баттл: три задачки, которые они умели решать и думали, что аналитически их не решить.
Если я правильно понял условия:
1)для данного треугольника построить 3 окружности внутри него, чтобы каждая окружность касалась двух сторой и двух других окружностей (окружности Мальфатти).
3)то жес самое для тетраэдра и четырёх сфер.
2)даны три точки. Надо окружность данного радиуса вписать в треугольник, каждая из сторон которого проходит через одну из выбранных точек.
из первой части сказания о итальянских математиках, как они жили в свои неспокойные времена разъединённой-под-оккупацией-объединяющейся Италией 19 века.
Если я правильно понял условия:
1)для данного треугольника построить 3 окружности внутри него, чтобы каждая окружность касалась двух сторой и двух других окружностей (окружности Мальфатти).
3)то жес самое для тетраэдра и четырёх сфер.
2)даны три точки. Надо окружность данного радиуса вписать в треугольник, каждая из сторон которого проходит через одну из выбранных точек.
из первой части сказания о итальянских математиках, как они жили в свои неспокойные времена разъединённой-под-оккупацией-объединяющейся Италией 19 века.
Красная и зеленая окружности касаются внешним образом.
Радиус зелёной равен 1.
Четыре равных отрезка показаны на рисунке.
1) Найдите радиус красной окружности
2) Найдите длину x тоже
Источник: https://www.facebook.com/groups/mathpuz/permalink/2278935512282278/
Радиус зелёной равен 1.
Четыре равных отрезка показаны на рисунке.
1) Найдите радиус красной окружности
2) Найдите длину x тоже
Источник: https://www.facebook.com/groups/mathpuz/permalink/2278935512282278/
«В древности было принято представлять факты элементарной геометрии в виде чертежей, без текста. В таком же ключе написана очень популярная среди школьников книжка А.Акопяна «Геометрия в картинках» (…). Но некоторые чертежи можно интерпретировать по-разному, т.е. на одном и том же чертеже можно увидеть различные факты.»
вот такая была небольшая статья А.Д.Блинкова в Кванте — http://mi.mathnet.ru/kvant3724
вот такая была небольшая статья А.Д.Блинкова в Кванте — http://mi.mathnet.ru/kvant3724
Задача от Петра Земскова
Пётр Александрович Земсков (учитель из Челябинска) ведёт в Youtube заслуженно популярный канал "Математика и фокусы". Недавно (на 1 сентября) он разбирал в нём такую вот геометрическую задачу
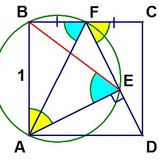
На сторонах единичного квадрата взяты произвольные точки (E,F,G), и построена пятиконечная звезда AFEDG. Оказалось, что площадь центрального (зеленого) пятиугольника равна 1/12. Найдите сумму площадей пяти красных треугольников.
1. Решите эту задачу.
2.* Исследуйте ее. Точно ли бывает у указанной площади значение 1/12? А какое максимальное значение она может принимать? Единственны ли те точки E,F,G, для которых достигается максимум? (если предполагать, что мы не меняем конфигурацию пятиугольника)
Пётр Александрович Земсков (учитель из Челябинска) ведёт в Youtube заслуженно популярный канал "Математика и фокусы". Недавно (на 1 сентября) он разбирал в нём такую вот геометрическую задачу
На сторонах единичного квадрата взяты произвольные точки (E,F,G), и построена пятиконечная звезда AFEDG. Оказалось, что площадь центрального (зеленого) пятиугольника равна 1/12. Найдите сумму площадей пяти красных треугольников.
1. Решите эту задачу.
2.* Исследуйте ее. Точно ли бывает у указанной площади значение 1/12? А какое максимальное значение она может принимать? Единственны ли те точки E,F,G, для которых достигается максимум? (если предполагать, что мы не меняем конфигурацию пятиугольника)
И еще одна задача, которую я придумал давным-давно, а сейчас вспомнил, потому что увидел у Земскова ее "родственника".
Дан треугольник ABC и точка D внутри него.
Докажите, что пять следующих условий (1) ∠DBC=30, (2) ∠ADB=150, (3) AC=AB, (4) AC=DC, (5) ∠DAB=∠DCB таковы, что из любых трех из них следуют остальные два.
Дан треугольник ABC и точка D внутри него.
Докажите, что пять следующих условий (1) ∠DBC=30, (2) ∠ADB=150, (3) AC=AB, (4) AC=DC, (5) ∠DAB=∠DCB таковы, что из любых трех из них следуют остальные два.