Фейсбук показал мой старый пост... Сюда я его точно не закидывал.
Инверсия линейкой
https://www.facebook.com/kostyaknop/posts/pfbid0YmCVLqa22JacJz3CbstwVpJYDyYTekJjArpP834VpmHH7JBTDqiimpyuUy7Cce7Rl
Инверсия линейкой
https://www.facebook.com/kostyaknop/posts/pfbid0YmCVLqa22JacJz3CbstwVpJYDyYTekJjArpP834VpmHH7JBTDqiimpyuUy7Cce7Rl
Forwarded from Mathpuz (Konstantin Knop)
A_1A_2...A_9 - правильный девятиугольник. Обозначим X_{klmn} точку пересечения диагоналей A_kA_m и A_lA_n.
1. Докажите, что P=X_{2679} и Q=X_{2349} лежат на прямой, параллельной стороне A_1A_9.
#medium
2. Докажите, что центр девятиугольника лежит на отрезке PQ.
#medium - #hard
3. Сколько всего точек пересечения диагоналей этого девятиугольника лежат на прямой PQ?
#hard
1. Докажите, что P=X_{2679} и Q=X_{2349} лежат на прямой, параллельной стороне A_1A_9.
#medium
2. Докажите, что центр девятиугольника лежит на отрезке PQ.
#medium - #hard
3. Сколько всего точек пересечения диагоналей этого девятиугольника лежат на прямой PQ?
#hard
Forwarded from Олимпиадная геометрия
This media is not supported in your browser
VIEW IN TELEGRAM
Для начинающих геометров.
Олимпиада им. Ясинского. Младшая лига, уровень Advanced, задача 2. Автор: Дмитрий Швецов
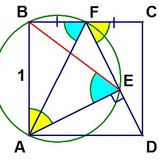
Точка X — произвольная точка на стороне AD квадрата ABCD. Докажите, что прямая, соединяющая точки касания вписанной окружности треугольника ABX со сторонами AX и BX проходит через центр квадрата.
Олимпиада им. Ясинского. Младшая лига, уровень Advanced, задача 2. Автор: Дмитрий Швецов
Точка X — произвольная точка на стороне AD квадрата ABCD. Докажите, что прямая, соединяющая точки касания вписанной окружности треугольника ABX со сторонами AX и BX проходит через центр квадрата.
Forwarded from Олимпиадная геометрия
Еще одна хорошая тренировочная задача. Baltic Way-2022. Задача 13.
Вписанный четырехугольник ABCD таков, что AB<BC и AD<DC. На сторонах BC и CD отмечены точки E и F соответственно такие, что AB=BE, AD=DF. Точка M — середина отрезка EF. Докажите, что прямые BM и DM перпендикулярны
Вписанный четырехугольник ABCD таков, что AB<BC и AD<DC. На сторонах BC и CD отмечены точки E и F соответственно такие, что AB=BE, AD=DF. Точка M — середина отрезка EF. Докажите, что прямые BM и DM перпендикулярны
Forwarded from Математическая вертикаль. РЦ Интеллектуал
Запись лекции для учителей
Выложили на ютуб-канал запись лекции Максима Анатольевича Волчкевича про геометрические построения, которая прошла 29 октября. Максим Анатольевич рассказал про обновленный учебник для 7 класса, показал примеры упражнений и разобрал задания, которыми можно заинтересовывать школьников.
Запись: https://youtu.be/cDFiz2Tp6rQ
Выложили на ютуб-канал запись лекции Максима Анатольевича Волчкевича про геометрические построения, которая прошла 29 октября. Максим Анатольевич рассказал про обновленный учебник для 7 класса, показал примеры упражнений и разобрал задания, которыми можно заинтересовывать школьников.
Запись: https://youtu.be/cDFiz2Tp6rQ
YouTube
Построения 7 кл. Волчкевич Максим Анатольевич. Лекции для учителей математики.
Forwarded from Олимпиадная геометрия
Всем привет! Опять про бабочек! Так внезапно получилось, что я сегодня выступаю на открытом семинаре Фоксфорда. На самом деле я выступал там и неделю назад, и рассказывал о некоторых самых интересных доказательствах теоремы о бабочке по мотивам видео, которое ранее публиковал на канале. А сегодня будет продолжение и я расскажу вещи, которые в видео не вошли: о задачах, которые решаются с помощью теоремы о бабочке и об доказательствах обобщений. Видео с первой серией доклада ниже, ссылка на зум появится в комментариях. Доклад начнется в 20-00 по московскому времени.
https://youtu.be/RM85xWmCKiM
https://youtu.be/RM85xWmCKiM
Forwarded from Непрерывное математическое образование
https://mccme.ru/nir/seminar/
уже 5-й год в МЦНМО работают кружки по геометрии
в четверг (24.11) на семинаре учителей Т.Корчемкина будет в основном рассказывать про кружок этого года, посвященный движениям
19:00, столовая МЦНМО,
приглашаются, как обычно, все желающие
уже 5-й год в МЦНМО работают кружки по геометрии
в четверг (24.11) на семинаре учителей Т.Корчемкина будет в основном рассказывать про кружок этого года, посвященный движениям
19:00, столовая МЦНМО,
приглашаются, как обычно, все желающие
Алексей Сгибнев провёл семинар для учителей про экспериментальные задачи по планиметрии на Матконструкторе.
https://urok.1c.ru/news/189290/
https://urok.1c.ru/news/189290/
Геометрия-канал
https://mccme.ru/nir/seminar/ уже 5-й год в МЦНМО работают кружки по геометрии в четверг (24.11) на семинаре учителей Т.Корчемкина будет в основном рассказывать про кружок этого года, посвященный движениям 19:00, столовая МЦНМО, приглашаются, как обычно…
Точки X, Y, Z лежат на одной
прямой, треугольники XBA, YBC, ZDC равносторонние (и расположены как на рисунке). Доказать, что AC и BD пересекаются на прямой XY.
(Задача про повороты с сегодняшнего… точнее, уже вчерашнего кружка.)
прямой, треугольники XBA, YBC, ZDC равносторонние (и расположены как на рисунке). Доказать, что AC и BD пересекаются на прямой XY.
(Задача про повороты с сегодняшнего… точнее, уже вчерашнего кружка.)
Forwarded from Общий знаменатель
Как с помощью единичного квадрата, слепой линейки и достаточно большого циркуля отмерить квадратный корень из любого натурального числа
#реклама
📚 Собираешься сдавать ЕГЭ по физике и профильной математике?
Бесплатно подготовиться поможет Академия карьеры ЕВРАЗа.
✅ Тебя ждут:
— Бесплатные регулярные занятия для подготовки к ЕГЭ
— Дополнительный курс профориентации
— Знакомство с деятельностью ЕВРАЗа
— Возможность получать дополнительную стипендию при поступлении в СибГИУ или НТИ УрФУ, а также гарантированное трудоустройство в компанию ЕВРАЗ.
Регистрируйся на программу и готовься к ЕГЭ вместе с ЕВРАЗом 👉🏻 https://vk.cc/cj7LJo
📚 Собираешься сдавать ЕГЭ по физике и профильной математике?
Бесплатно подготовиться поможет Академия карьеры ЕВРАЗа.
✅ Тебя ждут:
— Бесплатные регулярные занятия для подготовки к ЕГЭ
— Дополнительный курс профориентации
— Знакомство с деятельностью ЕВРАЗа
— Возможность получать дополнительную стипендию при поступлении в СибГИУ или НТИ УрФУ, а также гарантированное трудоустройство в компанию ЕВРАЗ.
Регистрируйся на программу и готовься к ЕГЭ вместе с ЕВРАЗом 👉🏻 https://vk.cc/cj7LJo
Forwarded from Mathpuz (Konstantin Knop)
Про задачу Паппа-Кастильона
Я тут открыл для себя забавную геометрическую задачу. Даны три точки A,B,C, лежащие на одной прямой. Требуется провести через них такие три прямых, чтобы точки их попарного пересечения лежали на данной окружности.
На картинке приведено геометрическое решение, - построение, которое я попробую максимально подробно описать. Самое интересное в нем то, что оно выполняется без циркуля, то есть одной геометрической линейкой.
Я тут открыл для себя забавную геометрическую задачу. Даны три точки A,B,C, лежащие на одной прямой. Требуется провести через них такие три прямых, чтобы точки их попарного пересечения лежали на данной окружности.
На картинке приведено геометрическое решение, - построение, которое я попробую максимально подробно описать. Самое интересное в нем то, что оно выполняется без циркуля, то есть одной геометрической линейкой.
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2023/zaoch_2023.pdf
https://geometry.ru/olimp/2023/zaoch_eng_2023.pdf
начинается заочный тур XIX олимпиады им. И.Ф.Шарыгина
24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
https://geometry.ru/olimp/2023/zaoch_eng_2023.pdf
начинается заочный тур XIX олимпиады им. И.Ф.Шарыгина
24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
Forwarded from Математическая вертикаль. РЦ Интеллектуал
Творческий семинар учителей математики при МЦНМО
8 декабря в 19:00 в столовой МЦНМО пройдет семинар с Дмитрием Викторовичем Прокопенко по теме «Доказательство некоторых классических формул. Дополнительные построения».
Подробнее: https://vertical.sch-int.ru/tvorcheskij-seminar-uchitelej-matematiki-pri-mcnmo/
8 декабря в 19:00 в столовой МЦНМО пройдет семинар с Дмитрием Викторовичем Прокопенко по теме «Доказательство некоторых классических формул. Дополнительные построения».
Подробнее: https://vertical.sch-int.ru/tvorcheskij-seminar-uchitelej-matematiki-pri-mcnmo/
Forwarded from Непрерывное математическое образование
Хорошо известно, что множество точек, из которых данный отрезок виден под прямым углом — это окружность (ну может без двух точек).
Менее известно, что отрезок можно заменить на эллипс. (Задача: доказать, что множество точек, из которых данный эллипс виден под прямым углом — это окружность. Заодно можно изучить, что будет, если заменить эллипс на гиперболу или на параболу.)
Менее известно, что отрезок можно заменить на эллипс. (Задача: доказать, что множество точек, из которых данный эллипс виден под прямым углом — это окружность. Заодно можно изучить, что будет, если заменить эллипс на гиперболу или на параболу.)
Forwarded from Олимпиадная геометрия
XXV кубок памяти А.Н. Колмогорова завершился личной олимпиадой. В юниорской лиге предлагалась очень соблазнительная задача номер 6.
В неравнобедренном остроугольном треугольнике ABC через ортоцентр H проведена прямая, перпендикулярная биссектрисе угла A, пересекающая стороны AB и AC в точках D и E соответственно. Пусть X — вторая точка пересечения описанных окружностей треугольников BDH и HEC. Докажите, что описанная окружность треугольника AHX касается биссектрисы угла BAC.
В неравнобедренном остроугольном треугольнике ABC через ортоцентр H проведена прямая, перпендикулярная биссектрисе угла A, пересекающая стороны AB и AC в точках D и E соответственно. Пусть X — вторая точка пересечения описанных окружностей треугольников BDH и HEC. Докажите, что описанная окружность треугольника AHX касается биссектрисы угла BAC.