Добрый день. Во вторник, 11 февраля в 15:30-16:30 по Москве, будет математический кружок 🍩

Title: Квадраты вокруг многоугольников

Speaker: Федор Нилов

Аннотация:

В геометрических конструкциях зачастую оказывается интересным строить на сторонах произвольного многоугольника правильные многоугольники, например, в теоремах Пифагора, Наполеона, Тебо, Ван Обеля. Мы обсудим свойства конструкции из бесконечного числа слоев квадратов вокруг некоторых многоугольников и красивую идею шарнирного доказательства.


Zoom meeting link:
Zoom - Meeting ID: 853 1771 8785 Passcode: 549695
Link: https://us02web.zoom.us/j/85317718785?pwd=XS0bILZaREyt00pA2EJlu1zxaEHbDN.1

Приходите!

пусть и вас позабавит несложное

Пусть O — центр описанной окружности треугольника ABC. Проведем через середину BC прямую параллельно OA и т.д. Почему такие три прямые пересекаются в одной точке — и что это за точка?

Классическая олимпиадная задача (было бы интересно узнать источник):

Для каких n существует замкнутая n-звенная ломаная, которая пересекает каждое свое звено ровно один раз?

Несложно понять, что ответ: при любых четных n>4.

Назовем две ломаных эквивалентными, если их вершины можно сопоставить друг другу таким образом, чтобы два звена одной ломаной пересекались тогда и только тогда, когда пересекаются звенья, соединяющие соответствующие звенья другой ломаной. Сколько может быть неэквивалентных друг другу ломаных при разных n, удовлетворяющих условию изначальной задачи?

P.S. На картинке герб ЮМШ

https://vkvideo.ru/video-163532021_456239221
https://vkvideo.ru/video-163532021_456239223

А.Д.Блинков рассказывает про задачи на построение

На стороне AB треугольника ABC отметили точку M так, что AM=BC. Из точек M и B на сторону AC опустили перпендикуляры MK и BH (см. рис.). AC вдвое больше KH. Угол A равен 22 градусам. Найдите угол C.

(задача Максима Волчкевича с сегодняшнего Матпраздника — доступна начинающим)

Via @don_schijuan

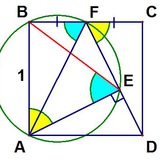
Центры вписанных коник изогонально сопряжены => точки касания лежат на 1 окружности

Друзья! Напоминаю, что сейчас и до конца марта идёт первый турнир нового сезона Квантландия с интерактивными задачами и головоломками. В этот раз мы сделали отдельно Турниры для 4-6 класса и для 7-9 класса, но участвовать могут и взрослые. Участие бесплатное, достаточно зарегистрироваться на сайте турнира https://math.kvantland.com/ и приступить к задачам (можно возвращаться к задачам в другой день и брать подсказки). Важно: лучше использовать ноутбук (не смартфон) и при регистрации на турнир на сайте использовать не gmail-почту, а альтернативную (yandex, mail,…), так как на gmail часто не приходит подтверждение регистрации. По итогам сезона мы наградим победителей!

Ну а сегодня задача по геометрии из предыдущего турнира для 7-9 класса:
На гипотенузе AB прямоугольного треугольника ABC отмечена точка D, из которой опущен перпендикуляр DE на катет BC. Найдите угол BCD, если AC = CD + DE, а угол CAE равен 23°.
Подписаться на Телеграм-канал
#Новости #ГеометрияДляВсех

В пространстве дан трехосный эллипсоид. Найти геометрическое место точек, из которых его контур виден, как круг. Иначе говоря, найти геометрическое место вершин круговых конусов, описанных около данного эллипсоида.

Квантик нарисовал выпуклый многоугольник и легко заштриховал его, проводя отрезки с концами на сторонах многоугольника.

Потом он подумал – а можно ли заштриховать любой выпуклый многогранник (вместе с внутренностью), проводя отрезки с концами на его рёбрах? Или для каких-то многогранников это не удастся и внутри останутся незаштрихованные пустоты?

// коллега Дориченко рассказал задачку