а) Стороны треугольника T2 на 1 больше соответствующих сторон треугольника Т1. Обязательно ли треугольник Т1 можно накрыть треугольником Т2?

б) Даны два тетраэдра; каждое ребро второго тетраэдра длиннее соответствующего ребра первого ровно на метр. Обязательно ли внутри второго тетраэдра можно разместить тетраэдр, равный первому? (Точкам нового тетраэдра разрешено попадать на границу второго.)

// А.Акопян по мотивам Р.Шварца; via https://tttttt.me/matheduks/207

Почему-то люблю эту задачу. Дан треугольник ABC. Окружность w касается сторон AB и AC и (ABC). Биссектриса угла ABC пересекает AC и (ABC) в точках X и Y. Докажите, что (AXY) касается w.

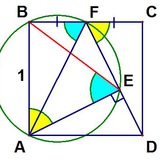
еще одна теорема о замыкании: если кругов четное количество, то цепочка на картинке замыкается за один круг (а если нечетное — за два круга)

// из https://arxiv.org/abs/2502.15751 via Д.А.Терешин

Еще одна задачка про красную окружность. Дан треугольник ABC с вписанной окружностью w. Биссектриса угла ABC пересекает AC и (ABC) в точках X и Y. Касательная параллельная BC к w пересекает (AXY) в точке T. Докажите, что YT касается w.

(СПБ-МО 2025 10.2)
Дан угол с вершиной A, величина которого меньше 180, и
число s > 0. На сторонах угла выбирают точки B и C так, что
площадь треугольника ABC равна s. Докажите, что существуют
такие точки X и Y (не зависящие от выбора точек B и C), что
точки B, C, X, Y всегда лежат на одной окружности.

Ладно. Для тех кому кажется что это простая задача есть пункт b. Докажите, что существует еще две таких точки X и Y только они всегда мнимые)

в новом Кванте (№1 за 2025 год) статья П.Кожевникова о теореме Понселе и возникающих инвариантах

в качестве анонса — вот первая страница

upd: https://www.mathnet.ru/rus/kvant4535

Геометрия на клетчатой бумаге это здОрово! Автор олимпиадных задач, учитель математики школы “Летово” и создатель проекта “Беседы” Дмитрий Викторович Швецов провёл короткую интерактивную лекцию для детей и взрослых на Фестивале Квантика.

Youtube: https://youtu.be/2SRpIZ8qAS8
VK-video: https://vk.com/video-223907838_456239083

Одна из красивых задач с этой лекции была такой:
У вас есть клетчатый лист бумаги со стороной клетки 1 и линейка. Как построить квадрат площади 4/5?
Решения присылайте в комментариях, но не забывайте их скрывать!
#ГеометрияДляВсех #Видеоразборы

оставлю здесь видеорассказ про переход от окружностей к параболам и другим коникам и сопутствующую алгебру (по мотивам семинара учителей в прошедшем мае; не для экспертов, а в качестве такого введения):

https://youtu.be/rkkTCbaV-Wg

(вспомнилось по ассоциации с задачей https://tttttt.me/olympgeom/1656 из олимп. геометрии)

Стороны пятиугольника Понселе продолжили, провели описанные окружности образовавшихся треугольников и отметили их повторные точки пересечения. Тогда при вращении пятиугольника Понселе между вписанной и описанной окружностями данные точки двигаются по фиксированной (синей) окружности:

https://www.geogebra.org/classic/zzckughf