Forwarded from GetAClass - физика и здравый смысл
#математика
Представляем вашему благосклонному вниманию новый ролик «Очень красивая задача», и к такому названию трудно что-то добавить, кроме того, что эта задача геометрическая.
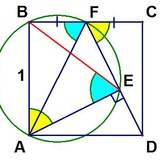
Вот её условие: точка внутри равностороннего треугольника соединена тремя отрезками с его вершинами, при этом оказалось, что сумма квадратов двух отрезков равна квадрату третьего. И требуется найти угол между первыми двумя отрезками.
Решить эту задачу можно буквально одним движением, попробуйте сделать это сами! И, конечно, смотрите наше решение и не забывайте ставить лайки!
P.S. По этой ссылке можно найти ролик на других платформах.
[Поддержите нас]
Представляем вашему благосклонному вниманию новый ролик «Очень красивая задача», и к такому названию трудно что-то добавить, кроме того, что эта задача геометрическая.
Вот её условие: точка внутри равностороннего треугольника соединена тремя отрезками с его вершинами, при этом оказалось, что сумма квадратов двух отрезков равна квадрату третьего. И требуется найти угол между первыми двумя отрезками.
Решить эту задачу можно буквально одним движением, попробуйте сделать это сами! И, конечно, смотрите наше решение и не забывайте ставить лайки!
P.S. По этой ссылке можно найти ролик на других платформах.
[Поддержите нас]
YouTube
Очень красивая задача
Красивая задача по геометрии решается с помощью поворота всей конфигурации на 60°.
Благодарим вас за интерес к нашей работе!
Получить доступ к дополнительным материалам можно в нашем телеграм-канале: https://tttttt.me/getaclass_channel
Если вам нравится то…
Благодарим вас за интерес к нашей работе!
Получить доступ к дополнительным материалам можно в нашем телеграм-канале: https://tttttt.me/getaclass_channel
Если вам нравится то…
1❤17🔥3👍1
Forwarded from Геометрия с Ниловым
Внутри правильного шестиугольника взяли другой правильный шестиугольник, после чего соединили их соответствующие вершины. Докажите, что сумма площадей красных четырехугольников равна сумме площадей синих шестиугольников. Верно ли, что сумма квадратов площадей красных равна сумме квадратов площадей синих?
1😁9❤5👎3👍1😐1
Forwarded from Ботаем геому
Условия прошедшей сегодня устной олимпиады по геометрии!
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
❤17👍3
Стартует спецкурс от Ивана Кухарчука и Леонида Шатунова на платформе Дабромат, будет про продвинутую геометрию в треугольнике, подробнее можно прочитать по ссылке, должно быть интересно.
Стоимость курса: 14 900 рублей
Стоимость курса: 14 900 рублей
dabromat.ru
Программа спецкурс Кухарчука
👎39❤6🔥5🤩4👍1🤓1
Forwarded from Олимпиадная геометрия
Слишком много дизлайков... Вот вам тогда задача с командной олимпиады проходящего сейчас Уральского турнира (63-го? я сбился со счета...)
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
❤16👎4👍3
Геометрия-канал
USEMO 2024 P3. Автор: Matsvei Zorka. Докажите равенство зеленых.
Давайте еще доп вопросик. Как построить точки P и Q?
❤4👍1
Геометрия-канал
USEMO 2024 P3. Автор: Matsvei Zorka. Докажите равенство зеленых.
Для тех кому эта задача кажется сложной. Есть более простая задача и очень полезная!
❤16👍3
Forwarded from Школа "Лес"
#онлайн_лекция
Друзья, 16 ноября в 18:00 по московскому времени состоится очередная онлайн-лекция нашего лектория!
На этот раз Полина Романова расскажет про то, как принципы геометрии используются в рисовании.
🔗 Трансляция произойдёт по этой ссылке.
⏰ Добавьте напоминание себе в календарь, чтобы не забыть.
Делитесь в комментариях своими любимыми скетчами с Инктобера, и до встречи в следующую субботу!
Друзья, 16 ноября в 18:00 по московскому времени состоится очередная онлайн-лекция нашего лектория!
На этот раз Полина Романова расскажет про то, как принципы геометрии используются в рисовании.
🔗 Трансляция произойдёт по этой ссылке.
⏰ Добавьте напоминание себе в календарь, чтобы не забыть.
Делитесь в комментариях своими любимыми скетчами с Инктобера, и до встречи в следующую субботу!
👍10❤2
Forwarded from Фулл и точка
YouTube
Geometry Belarus | #maths #math #mathematics #geometry #математика #геометрия #belarus
Приехали в гости в Беларусь
Таймкоды:
0:09 Начало
1:16 Задача Матвея
2:11 Переформулировка задачи Матвея
9:50 Почему угол 45
12:42 Конкурс!
Таймкоды:
0:09 Начало
1:16 Задача Матвея
2:11 Переформулировка задачи Матвея
9:50 Почему угол 45
12:42 Конкурс!
#красота_спасет_мир #разбор
Встречайте❗️Фантастический коллаб года 🔥
Специально для вас мы побывали в самом сердце белорусского олимпиадного математического движа 🧡— в гостях у крутейших авторов канала Geometry Belarus 😎
В этом выпуске ( тык - тык ) вас ждет авторский разбор одной из лучших (по версии Фулл и точка) геометрий года от легендарного призера международной математической олимпиады Матвея Зорько 🤩
Задача, которую мы будем разбирать, прогремела во всех геометрических пабликах, но для тех кто пропустил — условие и картинку мы оставляем в комментариях к посту 👇
Подумайте немного 🤔 прежде чем смотреть видео, чтобы получить настоящий кайф от неожиданного сюжетного поворота 😍
И как приятный бонус — в конце видео вас ждет конкурс с потрясающими белорусскими призами 🎁
Наливайте себе кружечку горячего чая ☕️, тыкайте на ссылочку 👉 тык - тык 👈
Прыемнага вам прагляду🎬
Встречайте❗️Фантастический коллаб года 🔥
Специально для вас мы побывали в самом сердце белорусского олимпиадного математического движа 🧡— в гостях у крутейших авторов канала Geometry Belarus 😎
В этом выпуске ( тык - тык ) вас ждет авторский разбор одной из лучших (по версии Фулл и точка) геометрий года от легендарного призера международной математической олимпиады Матвея Зорько 🤩
Задача, которую мы будем разбирать, прогремела во всех геометрических пабликах, но для тех кто пропустил — условие и картинку мы оставляем в комментариях к посту 👇
Подумайте немного 🤔 прежде чем смотреть видео, чтобы получить настоящий кайф от неожиданного сюжетного поворота 😍
И как приятный бонус — в конце видео вас ждет конкурс с потрясающими белорусскими призами 🎁
Наливайте себе кружечку горячего чая ☕️, тыкайте на ссылочку 👉 тык - тык 👈
Прыемнага вам прагляду
Please open Telegram to view this post
VIEW IN TELEGRAM
❤10👍6🔥3👎1
Forwarded from NeuroGeometry (Петр Ким)
Задача 56:
Автор - Григорий Забазнов
Источник: MGO 2024, задача 4
На сторонах AB и AC треугольника ABC выбраны точки E и F соответственно так,что B,E,F,C лежат на одной окружности. Прямые BF и CE пересекаются в точке K. Отражение прямой AK относительно биссетрисы угла BAC пересекает BF и CE в точках M и N.
Доказать, что если окружность (MKN) касается BC, то она касается и EF.
Автор - Григорий Забазнов
Источник: MGO 2024, задача 4
На сторонах AB и AC треугольника ABC выбраны точки E и F соответственно так,что B,E,F,C лежат на одной окружности. Прямые BF и CE пересекаются в точке K. Отражение прямой AK относительно биссетрисы угла BAC пересекает BF и CE в точках M и N.
Доказать, что если окружность (MKN) касается BC, то она касается и EF.
❤8👍1
Forwarded from Геометрия с Ниловым
Отношение длин касательных к эллипсу равно отношению радиусов вписанных окружностей (синих) и корню кубическому из отношения радиусов соприкасающихся окружностей (красных), касающихся эллипса в тех же точках. Второе утверждение - теорема Лиувилля.
👎7👍4❤2
Forwarded from Геометрия от Волчкевича
Верю — не верю!
Некоторые из предлагаемых шести утверждений на плоскости верны в общем случае. Отметьте их.
Некоторые из предлагаемых шести утверждений на плоскости верны в общем случае. Отметьте их.
Anonymous Poll
71%
1. У любого пятиугольника есть тупой угол.
38%
2. Шесть прямых могут иметь ровно 7 точек пересечения.
45%
3. Любую трапецию можно разрезать на две прямоугольные трапеции.
37%
4. Окружность, вписанная в треугольник со сторонами 4, 5 и 7, касается его средней линии.
46%
5. Сумма трех углов вписанного в окружность шестиугольника равна 360 градусов.
31%
6. Только правильный треугольник можно разрезать на три равных треугольника.
👍2❤1
Forwarded from Геометрия с Ниловым
Пусть X и Y - проекции ортоцентра H треугольника ABC на внутреннюю и внешнюю биссектрисы угла B. Докажите, что прямая XY проходит через середину стороны AC.
❤14👍3🤓1