Forwarded from Олимпиадная геометрия
Несколько фактов про точку касания полувписанной окружности
👍13❤7
Старая моя задача. На самом деле решаемая. Точки P выбираются внутри треугольника ABC так, что сумма зелёных = сумме красных. Точка Q - изогонально сопряжена точке P относительно ABC. Докажите, что PQ проходит через фиксированную точку.
🔥14👍2❤1
Forwarded from Олимпиадная геометрия
This media is not supported in your browser
VIEW IN TELEGRAM
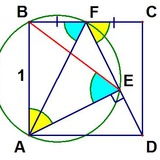
Добрая задача про параллелограмм
❤15🔥5
Forwarded from Быстрые задачки по математике (Alexey Sgibnev)
В треугольнике медиана и биссектриса перпендикулярны. Верно ли, что медиана делит биссектрису 3:1, считая от вершины?
Anonymous Quiz
64%
да
36%
нет
🔥5❤3😱3
Forwarded from Кроссворд Тьюринга (Vanya Yakovlev)
как коники, инволюции и геометрия Лобачевского помогают понимать задачи классической геометрии
На лекции будет рассказано о неожиданной связи классической школьной геометрии и конструкциях, которые традиционно считаются весьма далекими от тех, которые знакомы и известны школьникам.
Мы начнем с воспоминаний о прошедшем финале ВсОШ и обсудим решения задач 9.4 и 10.4 с помощью прямоугольных гипербол, поговорим о теореме Дезарга об инволюции и ее применении в задаче 11.4, а затем обсудим задачу, предлагавшуюся несколько лет назад участникам сборной России на Международную математическую олимпиаду, для понимания природы которой оказывается полезной геометрия Лобачевского.
В ходе лекции будут также поставлены открытые вопросы и проблемы, над которыми можно думать самостоятельно.
Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения). Также будет полезно знание определений конических сечений (эллипс, гипербола, парабола).
НАЧАЛО в 17:00 МСК/14:00 GMT
Ссылка на зум и все подробности в канале «Олимпиадной геометрии»
#анонс #открытые_лекции
Please open Telegram to view this post
VIEW IN TELEGRAM
YouTube
#1lec. П.В. Бибиков, Неевклидовы решения евклидовых задач
В лекции будет рассказано о неожиданной связи между евклидовой и неевклидовой геометриями. Оказывается, некоторые простые конструкции из геометрии Лобачевского позволяют быстро решать весьма трудные задачи из геометрии Евклида. Планируется рассказать о нескольких…
❤11👍3🔥1🥱1