Forwarded from Математические этюды
❤9👍4
Forwarded from Квантландия | Интересные задачи и не только
В этом году на базовом Турнире Городов в феврале было целых две задачи-картинки и обе от авторов Квантландии. Сегодня первая из них:
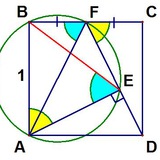
Произвольный прямоугольник разбит на прямоугольные треугольники так, как показано на рисунке ниже. В каждый треугольник вписан квадрат. Что больше: площадь красного квадрата или сумма площадей трёх зелёных?
Произвольный прямоугольник разбит на прямоугольные треугольники так, как показано на рисунке ниже. В каждый треугольник вписан квадрат. Что больше: площадь красного квадрата или сумма площадей трёх зелёных?
👍21❤6
Forwarded from Олимпиадная геометрия
Finally... Завтра 8-го марта с 17-00 до 21-00 по московскому времени я буду решать задачи заочного тура олимпиады Шарыгина.
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
Ориентируясь на опыт прошлого года, я решил, что я буду прорешивать все задачи подряд, но отводя на задачу не более 10 минут: если идей к решению не возникает — переключаюсь на следующую... А потом вернусь к задачам, которые не получились и буду уже думать над ними более предметно.
Буду рад, если вы присоединитесь, но понимаю, что завтра у многих выходной и вам может быть не до этого...
https://www.youtube.com/live/FBqr6JQgltM?si=gXKh4NKXhGsDJary
YouTube
#9str. Прорешиваем заочный тур олимпиады Шарыгина 2024
В этом стриме мы будем прорешивать задачи заочного тура олимпиады Шарыгина, который завершился на днях. Я буду делать это без предварительной подготовки в режиме онлайн.
❤15👍5🔥4
На боковых сторонах AB и BC равнобедренного остроугольного треугольника берут такие точки M и K, что угол MEA равен углу ABC (E — пересечение CM и AK). Доказать, что середины всевозможных отрезков MK лежат на одной прямой.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
// Такая задача М.Волчкевича предлагалась 8 классу на ММО сегодня. А если показалось слишком просто, то решите ту же задачу без условия равнобедренности треугольника ABC.
❤19🔥7👍4
Попробую сделать традицией выкладывать решения из чата в канал. Решение обобщение задачи выше.
👍8❤3🔥2
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2024/2024_zaoch_rus_sol.pdf
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
❤6
Forwarded from Квантландия | Интересные задачи и не только
А теперь вторая задача-картинка от авторов Квантландии (Е. Бакаев), которая совсем недавно была на базовом Турнире Городов:
Пять равносторонних треугольников расположены так, как показано на рисунке ниже. Три больших треугольника равны между собой, и два маленьких тоже равны между собой. Найдите углы треугольника ABC.
Пять равносторонних треугольников расположены так, как показано на рисунке ниже. Три больших треугольника равны между собой, и два маленьких тоже равны между собой. Найдите углы треугольника ABC.
❤12👍1
На плоскости нарисовали несколько окружностей, после чего отметили все точки их пересечения или касания. Оказалось, что на каждой окружности лежит ровно n отмеченных точек и через каждую отмеченную точку проходит ровно n окружностей. Чему может быть равно n?
🔥17❤3👍2😢1