Forwarded from Непрерывное математическое образование
https://artofproblemsolving.com/community/c3381519_2023imo
задачи 1 дня международной математической олимпиады-2023
задачи 1 дня международной математической олимпиады-2023
🔥14👍1
а) Доказать, что в любом треугольнике радиус описанной окружности хотя бы вдвое больше радиуса вписанной.
б) Сформулировать и доказать аналогичное неравенство для тетраэдров.
б) Сформулировать и доказать аналогичное неравенство для тетраэдров.
🤔13👍3❤1
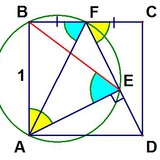
а) Окружность радиуса r лежит внутри окружности радиуса R, расстояние между центрами d. Доказать, что между ними можно расположить треугольник в точности при d²⩽R(R-2r).
б) Для тетраэдров в пространстве ответ на аналогичный вопрос d²⩽(R+r)(R-3r).
(Отсюда следует и предыдущая задача, но это не самый простой способ…)
// картинка — из https://arxiv.org/abs/1404.0525
б) Для тетраэдров в пространстве ответ на аналогичный вопрос d²⩽(R+r)(R-3r).
(Отсюда следует и предыдущая задача, но это не самый простой способ…)
// картинка — из https://arxiv.org/abs/1404.0525
❤11🤔5🔥1
Forwarded from Олимпиадная геометрия
Всем привет! Меня часто спрашивают, как научиться решать геометрические задачи? Какие есть материалы для самостоятельного изучения? Какие учебники вы посоветуете почитать? Я всякий раз отвечаю приблизительно одно и то же, но все же кажется полезным создать рубрику с рекомендациями, в которой я буду писать о полезных книгах и интересных геометрических статьях.
Одна из моих любимых книг по геометрии, с которой я познакомился будучи восьмиклассником, это книга Г.С.М. Коксетер, С.Л. Грейтцер "Новые встречи с геометрией" (по английски, кстати, называется "Geometry Revisited"). Произнося фамилию первого автора многие пропускают первую букву "е"... возможно, эти многие что-то знают об истинном произношении этой фамилии... Это одна из немногих книг, находящихся у меня в непосредственной близости от рабочего стола, поэтому прикладываю фотографию моего собственного экземпляра.
Одна из моих любимых книг по геометрии, с которой я познакомился будучи восьмиклассником, это книга Г.С.М. Коксетер, С.Л. Грейтцер "Новые встречи с геометрией" (по английски, кстати, называется "Geometry Revisited"). Произнося фамилию первого автора многие пропускают первую букву "е"... возможно, эти многие что-то знают об истинном произношении этой фамилии... Это одна из немногих книг, находящихся у меня в непосредственной близости от рабочего стола, поэтому прикладываю фотографию моего собственного экземпляра.
🔥21👍8❤4
Forwarded from Олимпиадная геометрия
H_S_M_Coxeter_S_L_Greitzer_Novye_vstrechi_s_geometriey_1978.djvu
2.4 MB
По большому счету эта книга составлена из популярных статей по геометрии – на мой взгляд, лучший из возможных для учебника стилей. Правда, в этой книге вы не найдете обилия задач... Зато среди предложенных тем есть практически все классические теоремы и содержательное введение в различные преобразования (движения, преобразования подобия, инверсии, проективные и полярные преобразования).
Пожалуй, именно в таком стиле я бы написал учебник, если бы когда-нибудь собрался это сделать...
На обложке книги изображена иллюстрация к доказательству Нараньенгару теоремы Морлея. Известное мне доказательство указанные окружности не использует... А вы сможете придумать доказательство с этими окружностями? Какие геометрические соотношения появляются на картинке благодаря окружностям?
Пожалуй, именно в таком стиле я бы написал учебник, если бы когда-нибудь собрался это сделать...
На обложке книги изображена иллюстрация к доказательству Нараньенгару теоремы Морлея. Известное мне доказательство указанные окружности не использует... А вы сможете придумать доказательство с этими окружностями? Какие геометрические соотношения появляются на картинке благодаря окружностям?
❤12🔥4👍3🤔3
напишите, какие из задач олимпиады Шарыгина понравились?
если ничего не решали, то можно для разминки решить, например, такую задачу (8-6):
При каких n можно замостить плоскость равными фигурами, ограниченными n дугами окружностей?
если ничего не решали, то можно для разминки решить, например, такую задачу (8-6):
При каких n можно замостить плоскость равными фигурами, ограниченными n дугами окружностей?
👍7
Forwarded from Непрерывное математическое образование
sharygin2023-final.pdf
45.8 KB
завершился финал 19-й олимпиады по геометрии имени И.Ф.Шарыгина — вот его задачи
решения, списки победителей-призеров скоро появятся на странице олимпиады, https://geometry.ru/olimp/2023.php
решения, списки победителей-призеров скоро появятся на странице олимпиады, https://geometry.ru/olimp/2023.php
👍11❤1
Четыре окружности попарно касаются. Доказать, что их кривизны (обратные радиусы) удовлетворяют соотношению (±a±b±c±d)²=2(a²+b²+c²+d²).
Дальше — можно попробовать обобщить на n-мерное пространство (это тоже сделал Содди… хотя, на самом деле, было известно и в 19 веке).
Дальше — можно попробовать обобщить на n-мерное пространство (это тоже сделал Содди… хотя, на самом деле, было известно и в 19 веке).
Forwarded from Не нравится
1371021a0.pdf
1.2 MB
>In 1936, the Nobel Prize-winning radiochemist Frederick Soddy noticed something odd as he built packings with Descartes’ relation. As the circles got smaller and curvatures bigger, he expected to get gnarly numbers with square roots or infinite decimals. Instead, all the curvatures were integers. This was a fairly straightforward consequence of Descartes’ equation, but nobody had noticed for hundreds of years. It inspired Soddy to publish a poem in the scientific journal Nature, which began:
>>For pairs of lips to kiss maybe
>>Involves no trigonometry.
>>’Tis not so when four circles kiss
>>Each one the other three.
А вы и дальше пытайтесь заслать статью в нейчур
>>For pairs of lips to kiss maybe
>>Involves no trigonometry.
>>’Tis not so when four circles kiss
>>Each one the other three.
А вы и дальше пытайтесь заслать статью в нейчур
😁8👍4👎1
Forwarded from Математическая эссенция
Даны два равновеликих (т.е. имеющих одинаковую площадь) многоугольника. Всегда ли возможно разрезать (прямолинейными разрезами) один многоугольник на такие части, из которых затем составить второй?
Ответ в статье "Равновеликость и равносоставленность".
Ответ в статье "Равновеликость и равносоставленность".
❤8👍1
Forwarded from Математическая эссенция
Теперь даны два равновеликих (имеющих одинаковый объём) многогранника. Всегда ли они равносоставленны? Этот вопрос гораздо сложнее вопроса о равносоставленности многоугольников. Ему посвящена статья"Инвариант Дена".
❤9
Forwarded from Олимпиадная геометрия
Я строил-строил и, наконец, построил!
https://youtu.be/TZ5xs9IjIHo
https://youtu.be/TZ5xs9IjIHo
YouTube
#36. Погружение в теорему Паскаля
В этом видео мы обсуждаем разнообразные доказательства теоремы Паскаля от самых элементарных до крайне содержательных
0:00 Intro
0:38 Формулировка
02:09 Первое доказательство: счет углов
04:06 Второе доказательство: радикальные оси
05:55 Третье доказательство:…
0:00 Intro
0:38 Формулировка
02:09 Первое доказательство: счет углов
04:06 Второе доказательство: радикальные оси
05:55 Третье доказательство:…
❤18👍6🔥3
Forwarded from Непрерывное математическое образование
картинки по выходным: два доказательства неравенства между средним арифметическим и средним геометрическим
❤44🔥6👍4
5 способов разделить отрезок на три равные части (красивые картинки от известного некоторым Vincent Pantaloni):
https://www.geogebra.org/m/xp7p9bzx
https://www.geogebra.org/m/xp7p9bzx
GeoGebra
Trisection d'un segment - 5 constructions
Cinq méthodes pour couper un segment en trois parties de même longueur.
👍26❤2🤔2🎉2
Forwarded from Геометрия от Волчкевича
Косинус угла
Вот моя новая задача для любителей оригами и тригонометрии. Известно, что отношение сторон листа бумаги для принтера в идеале должно быть равно √2. Возьмем такой идеальный лист, согнем его пополам, а затем два его угла совместим с серединой противоположной стороны. Косинус отмеченного на фото угла α будет рациональным числом. Можете сказать, какое это число?
Вот моя новая задача для любителей оригами и тригонометрии. Известно, что отношение сторон листа бумаги для принтера в идеале должно быть равно √2. Возьмем такой идеальный лист, согнем его пополам, а затем два его угла совместим с серединой противоположной стороны. Косинус отмеченного на фото угла α будет рациональным числом. Можете сказать, какое это число?
👍23❤6