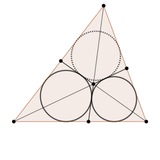
Задача от В.Н. Дубровского (извлечено из fb)

Доказать, что если BC и AD параллельны, то EC и AF тоже параллельны.

Вопрос от В.Н.:
This fact is the crucial point in a much more involved theorem, discussed in a number of papers, but I haven't seen it in such a concise form. Does anybody have a reference? Or an equally concise solution?

С удивлением вчера в очередной раз читал диспут про то, какие темы подходят, а какие не подходят для финала ВсОШ. Не слишком для меня удивительная особенность некоторых недавно выпустившихся и пока еще не выпустившихся:

до олимпиады недовольны тренировочными вариантами (в ваших тренировочных вариантах не те темы/не та сложность/задачи не того авторства — подчеркните нужное)

после олимпиады недовольны задачами олимпиады (в варианте олимпиады не те темы, что в были прошлые годы/не те темы, что проходят олимпиадники/не те темы, что проходят обычные школьники/слишком неразнообразное авторство/они бы еще ребус дали/они бы еще задачу на теорему Хана-Банаха дали — подчеркнуть нужное)

Кстати, про задачи на теорему Хана-Банаха. В 1998 году на финале ВсОШ была задача 11.8 авторства Алексея Яковлевича как раз на эту теорему.

Клетчатая фигура Ф обладает таким свойством: при любом заполнении клеток прямоугольника m×n числами, сумма которых положительна, фигуру Ф можно так расположить в прямоугольнике, чтобы сумма чисел в клетках прямоугольника, накрытых фигурой Ф, была положительна (фигуру Ф можно поворачивать). Докажите, что данный прямоугольник может быть покрыт фигурой Ф в несколько слоев.

Условия второго дня всеросса 2025

Задача 9.8, 10.8 просто удивительная!

В треугольнике ABC проведены две изогонали AD и AE (т.е. зеленые углы равны). Красные точки — центры описанных окружностей треугольников ABD, ABE, ACD и ACE. Синие точки — центры их окружностей девяти точек. Докажите, что красный и синий четырехугольники вписаны, подобны и коэффициент подобия равен 2.

Два эллипса и две гиперболы имеют общие фокусы. Докажите, что красные отрезки имеют одинаковую длину.

Добрая задача.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.

Эллипс "вписан" в окружность и к нему проведены две касательные. Докажите "теорему Брианшона".

в Квант №3 вошла статья «Угол между радиусом и стороной» Ю.Блинкова и Д.Швецова

2025 Taiwan TST Round 3 Mock P2

Классика, которая служит отправной точкой множеству сюжетов и идей в олимпиадной геометрии 👆

Задача 62:

Четырехугольник ABCD вписан в окружность с центром O. Лучи BA и CD пересекаются в точке E, а лучи AD и BC в точке F. Оказалось, что ED = FD. Докажите, что инцентры треугольников ADE и CDF равноудалены от O

Два красных отрезка равны. Докажите, что ортоцентр зеленого треугольника совпадает с центром описанной окружности синего (если синий треугольник не равнобедренный)