Еще одна задача из юниорской лиги. Мне нравится! Автор Алексей Доледенок.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы AB в точке D. Центр окружности — точка I. На луче DI выбрана точка E так, что ∠AEB = 45°.
Точки P и Q — основания перпендикуляров из E на стороны AC и BC соответственно. Описанная окружность треугольника DPQ пересекает стороны AC и BC в точках X и Y. Докажите, что AX = BY.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы AB в точке D. Центр окружности — точка I. На луче DI выбрана точка E так, что ∠AEB = 45°.
Точки P и Q — основания перпендикуляров из E на стороны AC и BC соответственно. Описанная окружность треугольника DPQ пересекает стороны AC и BC в точках X и Y. Докажите, что AX = BY.
Пост благодарности! Я бы хотел поблагодарить всех участников олимпиады за то, что они не поленились потратить свое воскресное время на решение задач, борьбу с лингвистическими и, порой, техническими трудностями, и это при том, что олимпиада эта не дает практически никаких бенефитов — без вас эта олимпиада была бы неполноценной.
Я бы хотел поблагодарить членов жюри, которые присоединились слушать задачи. Тоже ведь трудно заставить себя поучастовать в воскресном мероприятии, которое ничего кроме радости общения с единомышленниками тебе не принесет. Членам жюри тоже пришлось решать лингвистические и технические задачи, которые ставили перед ними участники. Спасибо вам! Хотелось бы, чтобы нас становилось больше и прослушка проходила в более спокойном режиме!
Я бы очень хотел поблагодарить авторов задач, которые не пожалели потратить свои творения на в общем-то никому пока неизвестную олимпиаду. В этом году, на мой взгляд, вариант получился значительно более интересным именно благодаря вам. Спасибо и тем, кто прислал свои задачи, но задачи нам почему-то не подошли. Я очень надеюсь, что вы не перестанете придумывать задачи и будете столь же отзывчивы на наши просьбы о помощи!
Я бы, конечно, хотел поблагодарить организаторов, потому что без их инициативы это мероприятие уж точно не состоялось бы. Организаторам всегда приходится не сладко, а работу их почти никто не видит.
Ну и конечно, я хотел бы поблагодарить своих коллег по методической комиссии!
Надеюсь олимпиада будет расти! И мы проведем ее еще лучше в следующем году. Пока что все задачи можно найти на аопсе. Но очень скоро мы доделаем и официальный файлик с условиями и решениями.
Я бы хотел поблагодарить членов жюри, которые присоединились слушать задачи. Тоже ведь трудно заставить себя поучастовать в воскресном мероприятии, которое ничего кроме радости общения с единомышленниками тебе не принесет. Членам жюри тоже пришлось решать лингвистические и технические задачи, которые ставили перед ними участники. Спасибо вам! Хотелось бы, чтобы нас становилось больше и прослушка проходила в более спокойном режиме!
Я бы очень хотел поблагодарить авторов задач, которые не пожалели потратить свои творения на в общем-то никому пока неизвестную олимпиаду. В этом году, на мой взгляд, вариант получился значительно более интересным именно благодаря вам. Спасибо и тем, кто прислал свои задачи, но задачи нам почему-то не подошли. Я очень надеюсь, что вы не перестанете придумывать задачи и будете столь же отзывчивы на наши просьбы о помощи!
Я бы, конечно, хотел поблагодарить организаторов, потому что без их инициативы это мероприятие уж точно не состоялось бы. Организаторам всегда приходится не сладко, а работу их почти никто не видит.
Ну и конечно, я хотел бы поблагодарить своих коллег по методической комиссии!
Надеюсь олимпиада будет расти! И мы проведем ее еще лучше в следующем году. Пока что все задачи можно найти на аопсе. Но очень скоро мы доделаем и официальный файлик с условиями и решениями.
Forwarded from Геометрия-канал (Grigory Merzon)
в «Олимпиадной геометрии» напомнили отличное утверждение
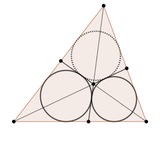
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
Forwarded from Геометрия-канал (Grigory Merzon)
mp-32-cubics.pdf
874.6 KB
Кубические кривые
и элементарная геометрия (А.Заславский, П.Кожевников; МатПросвещение, сер. 3, вып. 32)
тут неоднократно спрашивали, где можно прочитать про использование сложения точек на кубиках и т.п. в планиметрии — ну так вот
остальные материалы выпуска, кстати, тоже доступны — см. https://mccme.ru/free-books/matpros/pdf/mp-32.pdf
и элементарная геометрия (А.Заславский, П.Кожевников; МатПросвещение, сер. 3, вып. 32)
тут неоднократно спрашивали, где можно прочитать про использование сложения точек на кубиках и т.п. в планиметрии — ну так вот
остальные материалы выпуска, кстати, тоже доступны — см. https://mccme.ru/free-books/matpros/pdf/mp-32.pdf
Всем привет! Сегодня у одного нашего очень хорошего подписчика Вадима Калашникова день рождения. Я бы хотел его поздравить такой вот замечательной задачей.
Дан равносторонний шестиугольник ABCDEF. Докажите, что прямая, соединяющая ортоцентры треугольников ACE и BDF, параллельна прямой, соединяющей их центры описанных окружностей.
Дан равносторонний шестиугольник ABCDEF. Докажите, что прямая, соединяющая ортоцентры треугольников ACE и BDF, параллельна прямой, соединяющей их центры описанных окружностей.
Теорема Клера-Блисса
Через середины сторон треугольника проведены три синие параллельные прямые. Докажите, что прямые, симметричные сторонам относительно соответствующих синих прямых, пересекаются в одной точке. Найдите геометрическое место точек пересечения.
Ничего не значащий спойлер:
If we call the Minkowski perpendicular bisector of a segment with slope a the line through its midpoint with slope 1/a (the two lines are orthogonal in the Minkowski metric), the Klehr-Bliss theorem says that the Minkowski perpendicular bisectors of the three sides of a triangle are concurrent. The proof follows the usual proof: any point on the Minkowski perpendicular bisector of a segment is Minkowski equidistant from the two ends.
Через середины сторон треугольника проведены три синие параллельные прямые. Докажите, что прямые, симметричные сторонам относительно соответствующих синих прямых, пересекаются в одной точке. Найдите геометрическое место точек пересечения.
Ничего не значащий спойлер:
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2025/2025_zaoch_rus.pdf
https://geometry.ru/olimp/2025/2025_zaoch_eng.pdf
начинается заочный тур XXI олимпиады им. И.Ф.Шарыгина
как обычно: 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
https://geometry.ru/olimp/2025/2025_zaoch_eng.pdf
начинается заочный тур XXI олимпиады им. И.Ф.Шарыгина
как обычно: 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
Через центр O описанной окружности треугольника ABC проведена прямая, пересекающая стороны AB, BC и CA в точках F, D и E соответственно. Докажите, что окружности, построенные на AD, BE и CF как на диаметрах пересекаются в двух точках, одна из которых лежит на описанной окружности треугольника ABC, а вторая на окружности девяти точек.