Хочу начать ведение этого канала с задачи, которая мне очень нравится и близка. Как всегда в память западают красивые задачи, которые очень долго решал и в конце концов решил, получив от этого истинное наслаждение. Эта задача перекочевала из олимпиады в задачник нашего кружка, когда я был семиклассником, и более года ее никто не мог решить, хотя решение ее доступно любому, освоившему тему площади. Итак, задача.
Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.
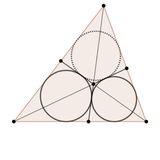
1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.
Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.
#геометрия #задачи #олимпиады #тургор #8класс #9класс
Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.
1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.
Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.
#геометрия #задачи #олимпиады #тургор #8класс #9класс
👍6❤2🔥2✍1🆒1
Всем привет! По случаю достижения 8000 подписчиков в группе вконтакте (вот бы такой прирост на YouTube!) публикую праздничный разбор, который давно обещал. Он короткий, но выполнен на совершенно ином уровне! Огромное спасибо JustMath за консультации по Manim.
А разбираем мы древнюю и очень красивую задачу с Турнира Городов 1994-го года.
#manim #тургор
https://youtu.be/pfORAIq-baU
А разбираем мы древнюю и очень красивую задачу с Турнира Городов 1994-го года.
#manim #тургор
https://youtu.be/pfORAIq-baU
YouTube
#21. Tournament of Towns - 1994, main variant, Problem 3
We consider very beautiful problem from the main variant of the Tournament of Towns-1994.
Let ABC be such a triangle with median AM that the equality AM + AC=AB holds. The incircle centered at I intersects median AM at points X and Y. Find the value of…
Let ABC be such a triangle with median AM that the equality AM + AC=AB holds. The incircle centered at I intersects median AM at points X and Y. Find the value of…
Forwarded from Олимпиадная геометрия
Хочу начать ведение этого канала с задачи, которая мне очень нравится и близка. Как всегда в память западают красивые задачи, которые очень долго решал и в конце концов решил, получив от этого истинное наслаждение. Эта задача перекочевала из олимпиады в задачник нашего кружка, когда я был семиклассником, и более года ее никто не мог решить, хотя решение ее доступно любому, освоившему тему площади. Итак, задача.
Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.
1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.
Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.
#геометрия #задачи #олимпиады #тургор #8класс #9класс
Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.
1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.
Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.
#геометрия #задачи #олимпиады #тургор #8класс #9класс
🎉49❤🔥11❤6👍3🤯2