Хочу начать ведение этого канала с задачи, которая мне очень нравится и близка. Как всегда в память западают красивые задачи, которые очень долго решал и в конце концов решил, получив от этого истинное наслаждение. Эта задача перекочевала из олимпиады в задачник нашего кружка, когда я был семиклассником, и более года ее никто не мог решить, хотя решение ее доступно любому, освоившему тему площади. Итак, задача.

Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.

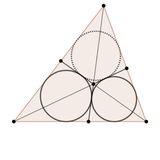
1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.

Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.

#геометрия #задачи #олимпиады #тургор #8класс #9класс

СПб, город, 1995,10.5
.
Следующая задача мне нравится потому, что она с одной стороны довольно сложная, а с другой доступна и семикласснику. Она предлагалась на городской олимпиаде 10-го класса под номером 5, то есть уже в выводной аудитории, что безусловно говорит о ее сложности.

Итак, задача.

#задачи #геометрия #олимпиады #спбмо #10класс #поворотнаягомотетия

Наш проект развивается после завершения конференции 🤟

Публикуем запись лекции про проективные коники.

🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴

Разговор про коники не только интересен, но еще и полезен!

Многие задачи по геометрии (в частности, с различных олимпиад) имеют очень короткое и естественное решение, использующее коники, несмотря на то, что кониками в их условии даже не пахнет 🤯

Яркий пример тому есть в нашем проекте — самое простое доказательство существования точки Шиффлера обычными методами занимает страницу текста, а вот при помощи равнобоких гипербол это делается буквально в одну строчку 🤩

Многих пугает новая теория, но бояться не стоит. Мы сделали так, чтобы разговор про коники был доступен каждому, кто увлекается обычной планиметрией)

Заваривайте себе кружечку горячего чая и кликайте сюда 👉 тык-тык 👈

Хочу начать ведение этого канала с задачи, которая мне очень нравится и близка. Как всегда в память западают красивые задачи, которые очень долго решал и в конце концов решил, получив от этого истинное наслаждение. Эта задача перекочевала из олимпиады в задачник нашего кружка, когда я был семиклассником, и более года ее никто не мог решить, хотя решение ее доступно любому, освоившему тему площади. Итак, задача.

Эта задача с Турнира Городов 94/95, осенний тур, 10-11.3.

1. Медиана AM треугольника ABC пересекает вписанную в него окружность в точках X и Y. Известно, что AB=AC+AM. Найдите угол XIY, если I - центр вписанной окружности треугольника.

Задача эта сложна тем, что абсолютно не понятно, как подступиться к точкам пересечения медианы и вписанной окружности. Однако намеком является соотношение на длины отрезков, данное в условии. Перед тем как читать решение я рекомендую вспомнить, как решается схожая, но более простая задача: если прямая, проходящая через центр вписанной окружности треугольника, делит его площадь пополам, то она делит пополам и его периметр.

#геометрия #задачи #олимпиады #тургор #8класс #9класс