Ладно, дам более точную формулировку про круги Кандинского. Эта задача сегодня всплыла в чате, но что-то на нее никто особо не отреагировал.

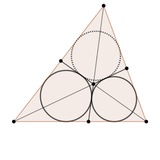
Дана классическая конструкция — четыре прямых и красные описанные окружности четырех образованных ими треугольников (красные окружности не нарисованы, но зато красным цветом отмечены их центры). Проводятся еще шесть черных окружностей: каждая проходит черех два красных центра и через точку пересечения соответствующих красных окружностей. Тогда все черные окружности равны. Источник: https://mathoverflow.net/questions/477497/twin-circles-in-a-quadrilateral

красная и синяя коники гомотетичны и пересекаются в двух точках. на их "радикальной оси", то есть прямой, соединяющей точки пересечения, выбрана точка, из которой проведены касательные к коникам (красные к красной, синие к синей). Докажите, что прямые, соединяющие красно-синие пары точек пересекаются в центре гомотетии.

Аналог задачи 255 для гиперболы.

Треугольник ABC описан около гиперболы. Докажите, что прямая, соединяющая точки касания гиперболы со сторонами CA и BC, средняя линия, параллельная стороне AC, и прямая, соединяющая вершину A с центром гиперболы, пересекаются в одной точке.

Для полноты картины аналогичный чертеж для параболы. Пунктирная прямая параллельна оси параболы

Это уже обсуждали как-то, но мне все равно очень нравится, поэтому не грех и повторить.

Две коники пересекаются по четырем точкам и отличаются поворотной гомотетией с углом поворота в 90 градусов. Докажите, что точки пересечения лежат на одной окружности.

Как мне указали в комментариях, поворотная гомотетичность не по делу. Достаточно параллельных осей...

Лемму о трезубце тоже можно сформулировать для гипербол.

Треугольник описан около двух гомотетичных гипербол (красная и синяя). Тогда треугольник вписан в гиперболу, гомотетичную первым двум, и проходящую через середину отрезка, соединяющего центры красной и синей гиперболы.

Вечернее упражнение: сформулируйте для гипербол лемму о велосипедистах

Готовясь к новому учебному году, изучал тут свои старые листики. Нашел листик про правильные многоугольники для не слишком обученных школьников. А там вот такая добрая задача, в которой нет никаких гипербол.

Три правильных 12-угольника расположены как показано на рисунке. Найдите углы выделенного треугольника.

Всем привет! Самое время начинать рассказывать про новый учебный год и разные проекты, в которых я планирую участвовать, и которые потенциально могут заинтересовать подписчиков этого канала.

Первый проект это Дабромат.

В этом году формат поменяется. Теперь Дабромат предлагает полноценное обучение на четырех уровнях (ступенях). На мой взгляд, на каждой ступени собралась очень крутой коллектив преподавателей (можете сами убедиться на сайте).

Я лично буду вести геометрию на третьей ступени (это приблизительно программа 9-го класса кружков). Раз в две недели вы будете получать листик по геометрии, решения я буду проверять через таксу Дусю и отправлять вам комментарии к вашим решениям, а по субботам будет разбор в зуме, где можно будет задавать все возникшие вопросы.

Руководителем третьей ступени является Илья Иванов-Погодаев

В общем, если ваш уровень соответствует третьей ступени обучения, мы будем рады видеть вас на нашем курсе!

Второй проект, в котором я буду участвовать в грядущем году это МТ-кружки. Эти онлайн кружки проходят в режиме гораздо более близком к традиционным. Два раза в неделю двухчасовые занятия, на которых можно решать задачи, отвечать задачи и слушать разборы. Своя группа в телеграме для каждого потока, много индивидуального общения, возможность все время быть в контакте с преподавателями и задавать вопросы (как на занятиях, так и вне).

В этом году я буду вести геометрические занятия в 9, 10 и 11 классах. Возможно, как и в прошлом году 10 и 11 классы будут объединяться на геометрические недели.

Как у нас устроены геометрические недели? Обычно я выбираю одну геометрическую тему и готовлю подборку из ориентировочно 15 задач, среди которых есть совсем базовые вещи, для тех, кто видит эту тему практически впервые, и есть глубокие задачи, для тех, кому нужен материал посложнее. Это позволяет погрузиться в тему и изучить ее на совершенно разном уровне, консультируясь при необходимости со мной. Я всегда готов подсказать по задаче, порекомендовать придумать альтернативный подход или наоборот выдать дополнительные материалы для изучения. Такой режим проведения занятий, конечно, для преподавателя более энергозатратный, но мне он гораздо ближе, поскольку позволяет лучше познакомиться со своими учениками и найти более индивидуальный подход.

Для примера в приложении прошлогодний листик про касание.

Интересная аналогия

все знают, что сумма расстояний от точки эллипса до фокусов постоянна

оказывается, фокусы можно заменить на любые дважды касающиеся эллипса окружности — докажите, что сумма синих касательных не зависит от выбора точки эллипса (upd: между точками касания… или нужно добавить знаки)

отсюда, кстати, следует и предыдущая задача

Наша коллега Вероника Молчанова как-то спросила одного из авторов канала — Ивана Кухарчука — какая его любимая задача по планиметрии. Он ответил тогда, что знает одну с польских национальных олимпиад

Задача. Дан четырехугольник, стороны которого или их продолжения касаются некоторой окружности. На его сторонах как на диаметрах построены четыре окружности. Докажите, что есть окружность, касающаяся этих четырех.

На наш вкус, это пример по-настоящему олимпиадной задачи:
🔥 чтобы решить задачу знать почти ничего не нужно,
🔥 решение очень непросто придумать даже профессионалу,
🔥 никакой техникой задача не бьется.

К тому же, решение короче, чем условие! И это притом, что само условие очень лаконично! 🤯

В итоге, Королёвские математические кружки, одним из ведущих преподавателей которых и является Вероника Геннадьевна, взяли себе логотип по мотиву этой задачи. А еще она появилась на королевских крУжках (см. видео в комментах 😉)

Листик про равносторонние треугольники для начинающих геометров

Чевианы AD, BE и CF пересекаются в точке P на описанной окружности треугольника ABC. Докажите, что описанные окружности треугольников ABC и DEF и окружность девяти точек треугольника DEF имеют общую радикальную ось.

В R^n существуют n+2 точки с целыми нечетными попарными расстояниями только если n имеет отстаток 14 от деления на 16. Об этом рассказывает Дима Крачун (см пересланное сообщение)

A tale of many distances:

Let us start from the very end, from the answer, the ultimate law of nature if you wish, and then gradually descend from the summit observing the views around.

Theorem: There exists a set of n+2 points in \R^n such that all pairwise distances between them are odd integers if and only if n is congruent to 14 modulo 16.

Arguably, looking at fourteen dimensions is somewhat justifiable given this is the answer, yet same cannot be said of distances being odd integers, for this restriction is, you know, odd. Hence, one might wonder if similar laws of nature exist in the realms less artificial, perhaps where all integers are treated with equal respect. It so happens that the answer is no, such a realm has infinitely many possibilities and virtually no restrictions, as seen by the following theorem.

Theorem: There exist arbitrary large non-trivial finite sets of points on the plane with all pairwise distances being integer. No such infinite set of points exists.

There is no cheating allowed, one could, of course, take all the points on the same line and claim the victory, so we deem all such examples trivial and concentrate on non-trivial ones. Ruling out the possibility of an infinite number of points is left to the reader and we briefly discuss the first half of the theorem.

The key to the construction lies in the famous theorem of Ptolemy giving a relation between the four sides and two diagonals of a cyclic quadrilateral and hence ensuring that if five distances between four points on a circle are rational, then so is the sixth one. We note in passing that by scaling we can indeed think of rational distances rather than integer ones. With such a hint we are naturally lead to consider a circle with diameter AB of unit length and an infinitude of points C_k on the circle at rational distances both from A and B given by various Pythagorean triples. Then |AC_k|, |BC_k|, |AB| are all rational by construction and |C_iC_j| are rational by the aforementioned theorem of Ptolemy. There are reasons to believe that possibilities are rather limited without Ptolemy, see [1, Theorem 1.1].

Having observed how dull the world of integer distances is, we return to the artificial world of odd restrictions to see how this world works. In spaces such as \R^n one has the benefit of scalar products, and so one natural step is to look at scalar products rather than distances: With n+2 points at odd distances in \R^n in mind we harmlessly assume that one of them, say A_0, is at the origin and look at scalar products <A_0A_i, A_0A_j>. Matrix with such entries, called Gramm matrix, has rank at most n (since all points are in \R^n) and hence zero determinant. Multiplying all entries by 2 and using the identity 2<a, b>=|a|^2+|b^2|-|a-b|^2, we see that 2<A_0A_i, A_0A_j> is congruent to 1 modulo 8 (recall that odd squares are congruent to 1 modulo 8 ) when i and j are distinct, whereas 2<A_0A_i, A_0A_i> = 2|A_0A_i|^2 is congruent to 2 modulo 16.

Claim: A symmetric m by m matrix with entries 2 on the diagonal and all other entries equal to 1 has determinant m+1. Modulo 16 the determinant does not change if one adds a symmetric matrix with all off-diagonal entries divisible by 8 and all diagonal entries divisible by 16.

Классная задача. Автор Van Khea из Камбоджи

Треугольник ABC вписан в окружность ω, на которой выбрана точка P. Окружность Ω касается ω в некоторой точке. Лучи PA, PB и PC пересекают Ω в точках D, E и F. Прямые D'E', E'F' и F'D' симметричны прямым DE, EF и FD относительно прямых AB, BC и CA соответственно. Докажите, что окружность, описанная около треугольника D'E'F' касается ω.

День красивых задач. Эта задача от Григория Борисовича Филипповского.

Источник t.me/geometry_ukraine

В треугольнике ABC проведена высота AD. Точки H и O — ортоцентр и центр описанной окружности треугольника ABC. Центр описанной окружности треугольника DHO отразили относительно HO. Докажите, что результат лежит на средней линии треугольника.