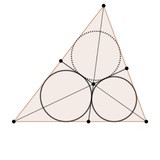
Приветствую. Заметил интересный факт: вершина треугольника A, соответствующая ей точка Шалтая P, симметричная A относительно точки Фейербаха A' и центр вписанной окружности I лежат на одной окружности. Предполагаю, что это известное утверждение. Буду признателен, если поделитесь интересными решениями.

Хотели бы сделать объявление:
С 18 по 23 августа на аопсе (ссылка ниже) будет проходить очень интересная олимпиада MGO 2024.

Составители задач - очень опытные геометры, среди них есть:
- Жюри олимпиады Шарыгина
- Золотые медалисты уровня Advanced Иранской геометрической Олимпиады
- Победители SAGF и Discord Geometry Olympiad
- Победители ВСОШ и кандидаты в сборную России на Международную Математическую Олимпиаду

Сложность задач будет достаточно высока: по шкале Imo Shortlist:
p1/p4 - G4
p2/p5 - G6/G7
p3/p6 - G8+

При этом в отличии от других олимпиад по геометрии высокой сложности на этой олимпиаде не будет:
- нагромождённых конструкций (все условия не более 4 строк в длину и обладают поразительной красотой)
- сложных объектов (каких-нибудь никому не известных замечательных точек, коник, или кубик)
- геометрических неравенств или комбинаторной геометрии

От себя могу добавить, что на мой взгляд, на этой олимпиаде будет несколько задач, которые могут претендовать на звание самых красивых задач в истории. Всем рекомендую поучаствовать!

https://artofproblemsolving.com/community/c594864h3379839_mgo_2024_announced

Про точку Шалтая тетраэдра можно думать так.

Пусть дан тетраэдр ABCD. Рассмотрим три сферы, касающиеся грани BCD в точках B, C и D и проходящие через вершину A. Докажите, что точка пересечения этих сфер, отличная от A, лежит на сфере, симметричной описанной около ABCD относительно грани BCD.

А какие еще свойства есть у такой точки?

а) Четырехугольник вписан в конику и описан вокруг коники. Теорема Понселе говорит, что тогда четырехугольник можно “вращать” с сохранением вписанности и описанности. Доказать, что точки пересечения противоположных сторон всё время лежат на одной прямой.

б) Полный четырехсторонник вписан в кубику и описан вокруг коники. Доказать, что четырехсторонник можно “вращать” с сохранением вписанности и описанности (предыдущий пункт соответствует кубике, распадающейся в объединение коники и прямой).

// via П.Бибиков: https://vk.com/wall840911_606

Предлагаю порешать такую задачу:
(источник - символ MGO, обобщение EMC 2022 S4, придуманное мной и Лёшей Суворовым)
Легко решается через линейную двигалку Кези, поэтому предлагаю поискать геометрические решения

сумма длин перпендикуляров из точки на стороны многоугольника Понселе не меняется

geometry_ukraine

Geometry Trip

https://youtu.be/QiaB6zubVws?si=LQCaWfTWMpUdLy6r

Наш проект развивается после завершения конференции 🤟

Публикуем запись лекции про проективные коники.

🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴🐴

Разговор про коники не только интересен, но еще и полезен!

Многие задачи по геометрии (в частности, с различных олимпиад) имеют очень короткое и естественное решение, использующее коники, несмотря на то, что кониками в их условии даже не пахнет 🤯

Яркий пример тому есть в нашем проекте — самое простое доказательство существования точки Шиффлера обычными методами занимает страницу текста, а вот при помощи равнобоких гипербол это делается буквально в одну строчку 🤩

Многих пугает новая теория, но бояться не стоит. Мы сделали так, чтобы разговор про коники был доступен каждому, кто увлекается обычной планиметрией)

Заваривайте себе кружечку горячего чая и кликайте сюда 👉 тык-тык 👈

Дан красный эллипс с красными фокусами и черная окружность. Докажите, что синяя пунктирная прямая касается эллипса.

Для окружности радиус в точку касания перпендикулярен касательной.

А что для эллипса: как связаны отрезок из фокуса в точку касания и перпендикуляр из фокуса на касательную? Простая задача: доказать, что красные отрезки параллельны.

// via Д.А.Терёшин via Stanley Rabinowitz

в качестве картинок по выходным — несколько кругов Кандинского

https://www.guggenheim.org/artwork/1992

Ладно, дам более точную формулировку про круги Кандинского. Эта задача сегодня всплыла в чате, но что-то на нее никто особо не отреагировал.

Дана классическая конструкция — четыре прямых и красные описанные окружности четырех образованных ими треугольников (красные окружности не нарисованы, но зато красным цветом отмечены их центры). Проводятся еще шесть черных окружностей: каждая проходит черех два красных центра и через точку пересечения соответствующих красных окружностей. Тогда все черные окружности равны. Источник: https://mathoverflow.net/questions/477497/twin-circles-in-a-quadrilateral

красная и синяя коники гомотетичны и пересекаются в двух точках. на их "радикальной оси", то есть прямой, соединяющей точки пересечения, выбрана точка, из которой проведены касательные к коникам (красные к красной, синие к синей). Докажите, что прямые, соединяющие красно-синие пары точек пересекаются в центре гомотетии.

Аналог задачи 255 для гиперболы.

Треугольник ABC описан около гиперболы. Докажите, что прямая, соединяющая точки касания гиперболы со сторонами CA и BC, средняя линия, параллельная стороне AC, и прямая, соединяющая вершину A с центром гиперболы, пересекаются в одной точке.

Для полноты картины аналогичный чертеж для параболы. Пунктирная прямая параллельна оси параболы

Это уже обсуждали как-то, но мне все равно очень нравится, поэтому не грех и повторить.

Две коники пересекаются по четырем точкам и отличаются поворотной гомотетией с углом поворота в 90 градусов. Докажите, что точки пересечения лежат на одной окружности.