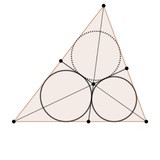
Пытался узнать, почему изодинамические центры так называются. Была у меня одна гипотеза, но она как-то не оправдалась. Видимо, такое название им дал Neuberg в сноске к статье про гармонический четырехугольник. Вообще там какой-то веселый источник в стиле "Решение задач по переписке + Статьи + задачи экзаменов", очень напоминает Квант, но без картинок...
🤝12✍5
Моя неоправдавшаяся гипотеза, почему изодинамические центры (точки Аполлония) так называются: это такие центры треугольника, которые сохраняются при инверсиях (а на самом деле и в более широком классе отображений плоскости). То есть если точки A, B, C перешли в точки A', B', C' то точка Аполлония треугольника ABC перешла в точку Аполлония A'B'C'.
🔥9🤯2✍1👍1
Прекрасные новости пришли с фронта умных чайников. AlphaProof решил все некомбинаторные задачи IMO-2024 и завоевал серебряную медаль!
https://www.newscientist.com/article/2441450-deepmind-ai-gets-silver-medal-at-international-mathematical-olympiad/
https://www.newscientist.com/article/2441450-deepmind-ai-gets-silver-medal-at-international-mathematical-olympiad/
New Scientist
DeepMind AI gets silver medal at International Mathematical Olympiad
AlphaProof, an AI from Google DeepMind, came close to matching the top participants in a prestigious competition for young mathematicians
❤23🤯12🔥2😁2🏆2✍1👏1
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
O,H - центр описанной окружности и ортоцентр оранжевого треугольника. У задачи есть очень изящное решение (как всегда)
👍15✍2
Фуф! Открытая неделя по барицентарам закончилась! Это был челлендж и для меня тоже, потому что кроме записи лекций и проведения разборов надо было еще и проверять много всего. За каждый плюсик участники получали по 100 даброкоинов, которые конвертировались прямо сегодня в рубли по курсу 1 дбк = 5,77 р. Их можно потратить на оплату интенсивной недели.
Сам интенсивный курс стартует уже завтра. Основной целью я ставлю рассказать, как можно классно работать с окружностями в барицентрических координатах. Это, кажется, мало кто знает)
Сам интенсивный курс стартует уже завтра. Основной целью я ставлю рассказать, как можно классно работать с окружностями в барицентрических координатах. Это, кажется, мало кто знает)
❤21🏆7🔥3👍2🌚1
Forwarded from Geometry Weekly
#51 (Окружной этап ВсОШ 2000, 11.3)
Доказать, что красная окружность касается MN
Доказать, что красная окружность касается MN
👍41✍7😍2👎1🤮1👌1🖕1
This media is not supported in your browser
VIEW IN TELEGRAM
Красный, синий и зеленый углы пропорциональны соответствующим углам треугольника. Точки пересечения называются точками Хофстедтера.
😁42✍14❤5❤🔥3👍2
Forwarded from Олимпиадная математика ВсОШ | Дабромат
⬜️ Финал олимпиады им. Шарыгина
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Фёдорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Фёдоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Фёдорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Фёдоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
✍20👍6🔥2❤1
Говорят, стартовала Летняя конференция Турнира Городов. Там есть классный геометрический проект про точки Шиффлера. Пока традиционно проект выложен не весь. Не знаю как вам, а мне прям интересно! Планирую пару вечеров посидеть-порешать. У проекта появился свой телеграм-канал, в котором, видимо, будут публиковаться иллюстрации к задачам и комментарии.
Что такое точка Шиффлера? Помните я как-то писал тут про факт, что если у четырех треугольников ABC, BCD, CDA и DAB три из прямых Эйлера проходят через одну точку, то и четвертая проходит через эту же точку. Так вот, если точка D=I — инцентр треугольника, то как раз выполняются условия и точка пересечения называется точкой Шиффлера треугольника. ГМТ точек D, для которых выполнено свойство, кстати, тоже по-своему интересно: оно состоит из описанной окружности треугольника, бесконечно удаленной прямой и кубики Нойберга.
В честь кого названа точка? Точка названа в честь любителя геометрии Курта Шиффлера, 1896-1996, (см. фото), основателя фирмы, которая специализируется на производстве игрушек, мебели и учебных материалов для детских садов.
Что такое точка Шиффлера? Помните я как-то писал тут про факт, что если у четырех треугольников ABC, BCD, CDA и DAB три из прямых Эйлера проходят через одну точку, то и четвертая проходит через эту же точку. Так вот, если точка D=I — инцентр треугольника, то как раз выполняются условия и точка пересечения называется точкой Шиффлера треугольника. ГМТ точек D, для которых выполнено свойство, кстати, тоже по-своему интересно: оно состоит из описанной окружности треугольника, бесконечно удаленной прямой и кубики Нойберга.
В честь кого названа точка? Точка названа в честь любителя геометрии Курта Шиффлера, 1896-1996, (см. фото), основателя фирмы, которая специализируется на производстве игрушек, мебели и учебных материалов для детских садов.
❤28🔥5🥰4✍2👍2🤯2❤🔥1🤝1
Forwarded from Математические кружки | «МТ кружки»
Новая 15-я задачная разминка «Поиск клада» — от нашего преподавателя Фёдора Львовича Бахарева. Его лаконичный комментарий:
Иногда задачи по геометрии имеют шутливую форму, но от этого не перестают быть содержательными. Наша первая разминка в этом сезоне — шуточно-геометрическая!
Будем рады увидеть в комментариях ваши решения или просто мысли о задачах!
Разбор задач будет проводиться Фёдором Львовичем в пятницу 9 августа в 18:00 мск по ссылке https://us06web.zoom.us/j/5634707332?pwd=TUcxTlJQbmxxMGRucDJ0ejVDaVZ3UT09&omn=83695771588
Присоединяйтесь!
#мт_разминка_продолжающие
Подписаться на «Математические кружки»
Please open Telegram to view this post
VIEW IN TELEGRAM
👍10❤3✍2
Одно из главных умений, которому надо научиться начинающему геометру, это понимать какие объекты на картинке зависят друг от друга, а какие нет. Зачастую это позволяет априори установить, что какой-то один угол выражается через какой-то другой, и на основании этого придумывать решение.
Одна из моих любимых задач на эту тему такая: доказать, что красные отрезки на картинке равны тогда и только тогда, когда равны синие.
Кидайте в комментариях задачи, где полезно разделить зависимости между объектами на картинке!
Одна из моих любимых задач на эту тему такая: доказать, что красные отрезки на картинке равны тогда и только тогда, когда равны синие.
Кидайте в комментариях задачи, где полезно разделить зависимости между объектами на картинке!
❤43👍12🥰9🔥7✍3💯1
Меня тут опять перепутали с другим Федором. На этот раз с Федей П. Это, конечно, очень лестно для меня, но теперь количество Федоров, с которыми меня можно перепутать, не столь уж велико. Если вы все еще нас путаете, то решите классическую задачу не по геометрии, придуманную задолго до того, как путать Федоров стало мэйнстримом.
😁81🔥6👍4💊2❤1🕊1🌚1
Я вот думаю, что если есть какое-то разумное утверждение про окружность, то оно должно быть в каком-то смысле верно и для равнобокой гиперболы.
На картинке треугольник описан около равнобокой гиперболы. Прямую, соединяющую две точки касания, пересекли с прямой, соединяющей третью с центром гиперболы. Докажите, что точка пересечения лежит на медиане треугольника.
На картинке треугольник описан около равнобокой гиперболы. Прямую, соединяющую две точки касания, пересекли с прямой, соединяющей третью с центром гиперболы. Докажите, что точка пересечения лежит на медиане треугольника.
☃19👍5🔥5❤4😱3