А вот еще задача про сумму радиусов.

Доказать, что радиус одного заштрихованного круга равен сумме радиусов двух других.

Квант М2793 (со звездочкой)

В остроугольном треугольнике ABC (AB <AC) точка O — центр описанной окружности. Пусть касательная к (ABC), проведенная в точке A, пересекает прямую BC в точке D. Пусть прямая DO пересекает отрезки AB и AC в точках E и F соответственно. Точка G построена так, что AEGF — параллелограмм. Пусть K и H — точки пересечения отрезка BC с отрезками EG и FG соответственно. Докажите, что окружность (GKH) касается окружности (ABC).

Чешско-Австрийско-Польско-Словацкий матч 2024 (растут!)

В четырехугольнике ABCD
AB=BC=CD. На лучах CA и BD выбрали точки X и Y соответственно так, что BX=CY. Докажите, что середины BX, CY, DX, AY лежат на одной окружности.

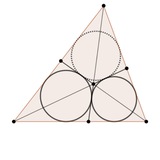
Очень часто вижу это утверждение как лемму в рассуждениях про окружности Мальфати. Но почему всегда оно считается в синусах? Я нашел здесь геом. решение... и мне оно показалось несложным, но забавным.

https://www.geogebra.org/geometry/yv4xupjq

В честь дня взятия Бастилии предлагаю вам задачу Дмитрия Терешина.

Есть довольно много задач с похожими картинками, в частности от Ламуна. Но большая часть из них так или иначе сводится к лемме о велосипедистах. С этой задачей это вроде бы не так...

На картинке даны три правильных пятиугольника. Доказать, что прямые пересекаются в одной точке.

что-то давно не было анимаций... эллипс, окружность и прямоугольник

IMO Shortlist 2023 G5

Условия IMO-2024

#48 (Сюжетик)

Фиолетовые окружности касаются двух сторон треугольника и его окружности девяти точек. Доказать, что их центры на одной прямой

Задача 52:
Автор - Ким Пëтр

В равнобедренном треугольнике ABC, AB = BC. Точка D на BC такова, что верно равенство углов: DAB = BAC. Точки X и Y на AB и BC соответственно таковы, что AX : XB = 2 : 1 и BY : XC = 2 : 1. Доказать, что отражение D относительно XY лежит на AC.

Когда-то на канале публиковал обобщение этой задачи. Но в такой формулировке тоже симпатично.

Равносторонний треугольник разбит на три треугольника: красный, синий и зеленый. Докажите, что их прямые Эйлера пресекаются в одной точке.

Так-так-так...

Оказывается уже на следующей неделе стартует спецкурс по барицентрическим координатам!

Точнее на следующей неделе стартует первая часть, в которой может поучаствовать любой желающий. Это хороший способ проверить, подойдет ли вам интенсив, который стартует неделей позже.

Что будет на открытой неделе? Мы повторим определение центра масс, проверим, что мы все хорошо понимаем, как массы группируются, как при помощи масс доказывать, что точки лежат на одной прямой или, что прямые пересекаются в одной точке. Посчитаем барицентрические координаты кое-каких точек. В качестве изюминки обсудим нотацию Конвея и лемму о диполе.

Для кого это подходит? Будет здорово, если вы придете с ненулевыми знаниями про массы, хотя все необходимые определения и теоремы я докажу на лекциях, так что при должном упорстве можно все освоить с нуля. Но уж конечно, нам не удастся обойтись без векторов.

Как будет проходить открытая неделя?
22-го лекция в записи + листик с задачами
24-го разбор в зуме в 17:30 мск
25-го лекция в записи + листик с задачами
27-го разбор в зуме в 17:30 мск
сдача задач письменная с моей проверкой через таксу Дусю

Что надо сделать, чтобы поучаствовать?
Перейти по ссылке. Зарегистрироваться. Заплатить 0 рублей. Не забыть поучаствовать, впрочем, наверняка, Дуся вам напомнит.

Буду рад вас видеть на спецкурсе и пообщаться с вами на разборах!

Кажется, появились результаты IMO-2024

Добрая, но красивая задача. Акопян геометрия в картинках 6.2.2.

Окружности W_1 и W_2 касаются окружности W внутренним образом в точках K_1 и K_2. Окружность Г_1 касается W_1 и касательных из K_1 к W_2. Окружность Г_2 определена аналогично. Докажите, что радиусы Г_1 и Г_2 равны.

Много геометрических каналов, конечно, развелось... проще перечислить тех, у кого их нет... но я попробую в почти случайном порядке перечислить те, что есть.

Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...

У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...

Кстати-кстати-кстати, спецкурс-то по барицентрическим координатам стартовал! Зарегистрировалось на открытую неделю пока всего 164 человека...

Первая лекция уже давно на платформе и многие начали присылать первые решения задач. Стараюсь оперативно все проверять... но сами понимаете...

Скажу вам по секрету, за решенные задачи на открытой неделе можно будет получить скидку на основной интенсив! Подробности ищите очень скоро на канале Олимпиадная математика ВсОШ.

Благодаря каналу Geometry Ukraine узнал некоторое время назад очень классную задачу про пару равносторонних треугольников с общей вершиной (см. картинку сверху — на ней отмечены центры треугольников).

А сегодня благодаря Кириллу узнал, что у задачи есть хорошее обобщение (картинка снизу). Два подобный треугольника сцеплены вершиной и на этот раз отмечены ортоцентры.

Всеми этими разговорами навеяло... две леммы о велосипедистах.