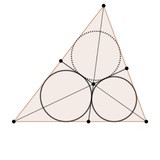
Какие еще есть доказательства теоремы Монжа?

Ну, во-первых, есть стандартное доказательство с теоремой Менелая. Я бы даже сказал, что теорема Монжа это и есть теорема Менелая.

Во-вторых, есть доказательство с композицией гомотетий. Если композиция трех гомотетий является тождественным преобразованием, то центры лежат на одной прямой. Как это понять? Надо проследить, например, за центром первой гомотетии. Если центры гомотетий не лежат на одной прямой, то он не имеет шансов вернуться назад в исходное положение.

В-третьих, есть замечательное доказательство от Григория Мерзона с линейными функциями. Обозначим центры окружностей A, B, C, их радиусы — a, b, c. Пускай [B,C] — линейная функция на плоскости, которая в точках B и C равна 0, а в точке A равна 1 (в частности, [B,C]=0 — уравнение линии центров этих окружностей). Аналогично определим функции [C,A] и [A,B].
Тогда a[B,C]+b[C,A]+c[A,B]=0 — уравнение прямой, на которой лежат нужные три точки.

В-четвертых, есть доказательство с моделью Пуанкаре плоскости Лобачевского. Вкратце, если радиусы (в смысле модели) первой и второй окружностей равны, и второй и третьей равны, то и радиусы первой и третей окружностей равны. А движение, переводящее равные окружности друг в друга это как раз гомотетия с центром на абсолюте.

В-пятых, есть доказательство Акопяна из вчерашнего поста.

А в-шестых, предлагаю такое доказательство с помощью масс. Пусть опять центры окружностей A, B, C, их радиусы — a, b, c. Поставим в точку A массу b-c, в точку B массу c-a, и в точку C массу a-b. Сумма масс равна нулю, центра масс нет, но есть утверждение, которое я называю лемма о диполе

Предположим дана система материальных точек с нулевой суммой масс. Ее разбили на две группы двумя способами. При первом разбиении образовалось две группы с ненулевыми суммами, при этом группа с положительной суммой масс имеет центром точку X+, а группа с отрицательной суммой масс имеет центром точку X-. При втором разбиении аналогично получаются точки Y+ и Y-. Тогда X-X+ и Y-Y+ параллельны - дипольная ось.

В нашем случае мы разобьем, скажем, массу в точке C на две

a-b=a/c(c-b)+b/c(a-c)

массы (A, b-c) и (C, a/c(c-b)) группируются в центр гомотетии окружностей с центрами A и C;

массы (B, c-a), (C, b/c(a-c)) группируются в центр гомотетии окружностей с центрами B и C;

поэтому прямая, соединяющая два центра гомотетий, параллельна дипольной оси нашей системы масс. а значит и все три центра лежат на одной прямой.

UPD. Забыл еще доказательство со сферами и выходом в пространство..

Хорошее упражнение из задачника В.В. Прасолова

Красная прямая пересекает две красные окружности в четырёх точках. Докажите, что касательные в этих точках к одной окружности пересекают касательные к другой окружности в четырёх точках, лежащих на окружности, причём центр этой окружности лежит на прямой, соединяющей центры данных окружностей.

А еще полезно вспомнить задачу П.А. Кожевникова с финала олимпиады Шарыгина 2021 года

Секущая пересекает первую окружность в точках A1, B1, а вторую — в точках A2, B2. Вторая секущая пересекает первую окружность в точках C1, D1, а вторую — в точках C2, D2. Докажите, что точки A1C1 ∩ B2D2, A1C1 ∩ A2C2, A2C2 ∩ B1D1, B2D2 ∩ B1D1 лежат на одной окружности, соосной с данными двумя.

https://arxiv.org/abs/2306.15099

А.Г.Хованский про центр масс в т.ч. для систем с нулевой суммарной массой (в этом случае он является не массивной точкой, а “диполем”)

В треугольнике ABC отмечена середина M высоты AH и центр вписанной окружности I. D — точка касания вписанной окружности со стороной BC. Зеленая точка — четвертая вершина отмеченного прямоугольника и центр зеленой окружности. Докажите, что зеленая окружность касается описанной.

Еще задача с тремя равными окружностями, но более простая. ELMO SL G2. Оказалось, что красные окружности равны. Надо доказать, что сумма радиусов красной и синий окружностей равна радиусу черной окружности.

А вот еще задача про сумму радиусов.

Доказать, что радиус одного заштрихованного круга равен сумме радиусов двух других.

Квант М2793 (со звездочкой)

В остроугольном треугольнике ABC (AB <AC) точка O — центр описанной окружности. Пусть касательная к (ABC), проведенная в точке A, пересекает прямую BC в точке D. Пусть прямая DO пересекает отрезки AB и AC в точках E и F соответственно. Точка G построена так, что AEGF — параллелограмм. Пусть K и H — точки пересечения отрезка BC с отрезками EG и FG соответственно. Докажите, что окружность (GKH) касается окружности (ABC).

Чешско-Австрийско-Польско-Словацкий матч 2024 (растут!)

В четырехугольнике ABCD
AB=BC=CD. На лучах CA и BD выбрали точки X и Y соответственно так, что BX=CY. Докажите, что середины BX, CY, DX, AY лежат на одной окружности.

Очень часто вижу это утверждение как лемму в рассуждениях про окружности Мальфати. Но почему всегда оно считается в синусах? Я нашел здесь геом. решение... и мне оно показалось несложным, но забавным.

https://www.geogebra.org/geometry/yv4xupjq

В честь дня взятия Бастилии предлагаю вам задачу Дмитрия Терешина.

Есть довольно много задач с похожими картинками, в частности от Ламуна. Но большая часть из них так или иначе сводится к лемме о велосипедистах. С этой задачей это вроде бы не так...

На картинке даны три правильных пятиугольника. Доказать, что прямые пересекаются в одной точке.

что-то давно не было анимаций... эллипс, окружность и прямоугольник

IMO Shortlist 2023 G5

Условия IMO-2024

#48 (Сюжетик)

Фиолетовые окружности касаются двух сторон треугольника и его окружности девяти точек. Доказать, что их центры на одной прямой

Задача 52:
Автор - Ким Пëтр

В равнобедренном треугольнике ABC, AB = BC. Точка D на BC такова, что верно равенство углов: DAB = BAC. Точки X и Y на AB и BC соответственно таковы, что AX : XB = 2 : 1 и BY : XC = 2 : 1. Доказать, что отражение D относительно XY лежит на AC.

Когда-то на канале публиковал обобщение этой задачи. Но в такой формулировке тоже симпатично.

Равносторонний треугольник разбит на три треугольника: красный, синий и зеленый. Докажите, что их прямые Эйлера пресекаются в одной точке.

Так-так-так...

Оказывается уже на следующей неделе стартует спецкурс по барицентрическим координатам!

Точнее на следующей неделе стартует первая часть, в которой может поучаствовать любой желающий. Это хороший способ проверить, подойдет ли вам интенсив, который стартует неделей позже.

Что будет на открытой неделе? Мы повторим определение центра масс, проверим, что мы все хорошо понимаем, как массы группируются, как при помощи масс доказывать, что точки лежат на одной прямой или, что прямые пересекаются в одной точке. Посчитаем барицентрические координаты кое-каких точек. В качестве изюминки обсудим нотацию Конвея и лемму о диполе.

Для кого это подходит? Будет здорово, если вы придете с ненулевыми знаниями про массы, хотя все необходимые определения и теоремы я докажу на лекциях, так что при должном упорстве можно все освоить с нуля. Но уж конечно, нам не удастся обойтись без векторов.

Как будет проходить открытая неделя?
22-го лекция в записи + листик с задачами
24-го разбор в зуме в 17:30 мск
25-го лекция в записи + листик с задачами
27-го разбор в зуме в 17:30 мск
сдача задач письменная с моей проверкой через таксу Дусю

Что надо сделать, чтобы поучаствовать?
Перейти по ссылке. Зарегистрироваться. Заплатить 0 рублей. Не забыть поучаствовать, впрочем, наверняка, Дуся вам напомнит.

Буду рад вас видеть на спецкурсе и пообщаться с вами на разборах!

Кажется, появились результаты IMO-2024

Добрая, но красивая задача. Акопян геометрия в картинках 6.2.2.

Окружности W_1 и W_2 касаются окружности W внутренним образом в точках K_1 и K_2. Окружность Г_1 касается W_1 и касательных из K_1 к W_2. Окружность Г_2 определена аналогично. Докажите, что радиусы Г_1 и Г_2 равны.