Исправление к одной из картинок. Там отрезок потерялся

Вот так выглядит контр-пример для теоремы Штейнера-Лемуса. В треугольнике с углами 12 и 36 градусов равны две биссектрисы внешних углов.

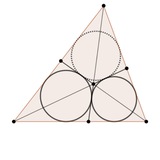
Хорошая, сравнительно добрая по нынешним меркам задача с питерского отбора 1995-го года. Автор: С.Л. Берлов.

На плоскости даны две пересекающиеся окружности. Точка A —‍ одна из двух точек пересечения. В каждой окружности проведён диаметр, параллельный касательной в точке A‍ к другой окружности, причём эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.

Напоминание!

Всем привет! Самое время для анонса! Почти ровно через две недели 14-го мая в 17:00 по московскому времени мы повторим эксперимент: на нашем канале состоится лекция Павла Витальевича Бибикова, на которой мы обсудим много интересного и нетривиального!

О неожиданных конструкциях в евклидовой геометрии: как коники, инволюции и геометрия Лобачевского помогают понимать задачи классической геометрии.

На лекции будет рассказано о неожиданной связи классической школьной геометрии и конструкциях, которые традиционно считаются весьма далекими от тех, которые знакомы и известны школьникам. Мы начнем с воспоминаний о прошедшем финале ВсОШ и обсудим решения задач 9.4 и 10.4 с помощью прямоугольных гипербол, поговорим о теореме Дезарга об инволюции и ее применении в задаче 11.4, а затем обсудим задачу, предлагавшуюся несколько лет назад участникам сборной России на Международную математическую олимпиаду, для понимания природы которой оказывается полезной геометрия Лобачевского. В ходе лекции будут также поставлены открытые вопросы и проблемы, над которыми можно думать самостоятельно.

Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения). Также будет полезно знание определений конических сечений (эллипс, гипербола, парабола).

Решал тут одну задачу и сделал удивительное (но не очень сложное) наблюдение. Кажется, годится в рубрику "оказывается".

Оказывается, если взять три красных окружности и их красный радикальный центр; отразить красные окружности относительно зеленой и получить синие окружности; найти синий радикальный центр синих окружностей, то центр зеленой окружности лежит на прямой, соединяющей радикальные центры.

Задача с олимпиады 239 1995-го года. Автор: С.Л. Берлов

В выпуклом четырёхугольнике ABCD‍ известно, что ∠A + ∠D = 120‍∘‍ и AB = BC = CD.‍ Докажите, что точка пересечения диагоналей равноудалена от вершин A‍ и D.‍

Всем привет! Сегодняшний стрим можно будет смотреть на Youtube. Присоединяйтесь в 17:00 по московскому времени!

https://youtube.com/live/KSsIn-tcA7Q?feature=share

Мы начинаем!

Хорошее и не очень сложное геометрическое неравенство.

M —‍ точка пересечения диагоналей вписанного четырёхугольника, N —‍ точка пересечения его средних линий (отрезков, соединяющих середины противоположных сторон), O —‍ центр описанной окружности. Докажите, что OM ≥ ON.‍

Продолжая тему радикального центризма...

Оказывается... Я знаю три утверждения для эллипсов, которые в каком-то смыле про "радикальный центр". Кажется, правое самое правильное, да?

Добрая задача от члена-корреспондента РАН Иванова С.В.

Дан выпуклый кайт ABCD (AB=AD, CB=CD) ∠BCD = 3∠ABD.‍ DE —‍ биссектриса треугольника ABD,‍ отрезки CE‍ и BD пересекаются в точке F.‍ Докажите, что треугольник BEF —‍ равнобедренный.