Главное, чтобы Нижний не стал для вас горьким)

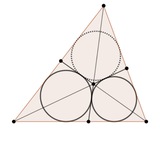
Даны синие окружности, тогда красная кривая — эллипс

Финал ВсОШ 2024, 9.6.

H — ортоцентр, O — центр описанной окружности. Доказать, что XY делит BC пополам.

Не очень свежая задача Финал ВсОШ 2024, 11.6

H — ортоцентр, O — центр описанной окружности. Доказать, что четыре точки лежат на пунктирной окружности, касающейся описанной окружности треугольника.

Довольно добрая задача 10.6.

Дан параллелограмм, красные отрезки равны, синие отрезки равны. Доказать, что есть пунктирная окружность.

Пока тут все были увлечены финалом, я рассказывал про задачу Мальфатти, точнее про точку Адзимы-Мальфатти. Придумал задачу, но что-то пока не очень решил...

Добрая задача с питерской олимпиады про равнобедренный треугольник.

1 и 2 день, решения

Выскажу еще свое непрошенное мнение по поводу геометрических задач на финале ВсОШ.

Во-первых, мне все задачи понравились. Я не увидел каких-то слишком уж вычурных или противоестественных конструкций. Может лишь геометрическое неравенство из 10-го класса мне не слишком зашло. Но, возможно, на это повлияла более симпатичная формулировка из 9-го класса.

Во-вторых, конечно, трудно не повторять какие-то уже знакомые сюжеты (это касается шестых задач). Всё-таки все геометрические задачи не упомнишь. Я, например, помню только те, которые часто выдаю. Вчера вот прислали в комментариях задачу с Сириус-курсов — я ее не помнил. Во всех же предложенных конструкциях были сделаны интересные наблюдения и в целом задачи симпатичные. А стандартность решения для задач с номерами 2 или 6 вполне себе, на мой взгляд, допустима.

В-третьих, я рад, что линейность разности степеней точки оказалась полезной в одной из задач. Я весь этот учебный год и прошлый пропагандировал эту идею среди тех, кого учил, и считаю, что это очень богатое направление. Задач, которые с помощью этой идеи решаются, будет еще много.

В-четвертых, я рад, что в официальных решениях перестали стесняться того, что задача может решаться, например, счетом в комплексных числах (увидел намеки на это в двух задачах). Возможно, когда-нибудь не будут и при составлении столько внимания уделять "отсутствию счетных решений".

Задача с Московской олимпиады, 2009.

Буквами H обозначены ортоцентры соответствующих треугольников.

Добрая задача с первого тура питерской олимпиады 9-го класса 2010 года.

ABCD — параллелограмм, M — середина AF, N — середина CE. Доказать, что если B, M и E на одной прямой, то и B, N, F тоже на одной прямой.

Есть, конечно, и очень короткое, но не очень доброе решение...

Первая теорема Сонда.

Два подобных треугольника ABC и A'B'C' таковы, что их соответственные стороны перпендикулярны, а точки пересечения соответственных сторон лежат на одной прямой (перспектриса). Тогда перспектриса делит пополам отрезок между ортоцентрами треугольников.

В одном модном сообществе в запрещенной в РФ сети, упоминают нашу добрую традицию. И задача совсем добрая: доказать, что alpha=beta, если DB не равно DC.

Добрый факт

Очень крутая задача с очень крутым решением. JBMO Shortlist 2022 G6. Proposed by Nikola Velov, Macedonia.

Что-то очень классическое...
Romanian TST 2004