На этой неделе на тренировках по геометрии повторяем и применяем поворотную гомотетию в контексте олимпиадных задач. Думаю, это будет полезно и для тех, кто совсем недавно узнал, что такое поворотная гомотетия, и для тех, кто уже какое-то время с ней прожил. Думаю, что это самая востребованная из базовых тем. Задачи, которые будем разбирать на этой неделе:
JBMO, Shortlist, 2014, G2
IMO, Shortlist, 2017, G1
APMO, 2015, P1
USAMO, 2008, P2
Устная ол. по геометрии, 2021, 8-9, P4
IMO, 2005, P5
IMO, Shortlist, 2015, G3
ВсОШ, 2019, 10.4
JBMO, Shortlist, 2014, G2
IMO, Shortlist, 2017, G1
APMO, 2015, P1
USAMO, 2008, P2
Устная ол. по геометрии, 2021, 8-9, P4
IMO, 2005, P5
IMO, Shortlist, 2015, G3
ВсОШ, 2019, 10.4
А вот вопрос к залу. Есть ли какие-то нормальные доказательства или правильные обобщения следующего факта?
Окружность, проходящая через основания биссектрис, высекает на сторонах треугольника три отрезка. Докажите, что один из них равен сумме двух других.
(У меня самого хоть счет и довольно изящный, но все-таки счет)
Окружность, проходящая через основания биссектрис, высекает на сторонах треугольника три отрезка. Докажите, что один из них равен сумме двух других.
(У меня самого хоть счет и довольно изящный, но все-таки счет)
Про более или менее изящный счет и какие-то геометрические мотивы в задаче про окружность через основания биссектрис. Возможно, кто-нибудь сможет развить идею в какое-нибудь относительно геометрическое соображение.
На картинке нарисован отрезок PQ, на нем точка X и окружность, проходящая через X и высекающая на PQ хорду длиной x. Тогда x можно найти по указанной формуле (x при этом обретет знак). Формула проверяется простой подстановкой, но эта подстановка совсем не обяъсняет никакой геометрической подоплеки.
Теперь в исходной задаче про треугольник все просто: отношение PX/QX переписывается через отношение соответственных сторон и все слагаемые приобретают вид
bc/a pow(A)
и, появляясь один раз с плюсом и один раз с минусом, успешно сокращаются. (Возможно, тут сокрыта какая-то вариация теоремы Карно).
Какая тут кажется может быть мораль? Надо бы придумать какое-то геометрическое объяснение формуле со скриншота. Мне кажется, не очень хорошей идея думать прямо про эту формулу и мне кажется, лучше из степени сделать линейную функцию. Для этого надо вычесть из нее что-то. Есть два хороших кандидата, которые приводят приблизительно к одному и тому же результату.
Первый кандидат — вычесть степень точки относительно какой-то окружности, проходящей через точки P и Q. Второй — вычесть степень точки относительно точки X.
В обоих случаях формула, которая получится, будет иметь вид
x= ... f(P) - ... f(Q)
Коэффициенты, обозначенные ... такие же как на скриншоте, относятся как (PX/QX)^2 и имеют разный знак, поэтому выражение сворачивается в формулу для f(O), где O — центр окружности Аполлония, построенной по точке X и отрезку PQ. (Кстати, у точки O степень относительно любой окружности, проходящей через P и Q как раз равна OX^2.)
На этом мысль у меня немного обрывается, но возможно, кто-то сможет предложить еще какую-то геометрическую идею, которая бы обяснила формулу и почему задача верна.
На картинке нарисован отрезок PQ, на нем точка X и окружность, проходящая через X и высекающая на PQ хорду длиной x. Тогда x можно найти по указанной формуле (x при этом обретет знак). Формула проверяется простой подстановкой, но эта подстановка совсем не обяъсняет никакой геометрической подоплеки.
Теперь в исходной задаче про треугольник все просто: отношение PX/QX переписывается через отношение соответственных сторон и все слагаемые приобретают вид
bc/a pow(A)
и, появляясь один раз с плюсом и один раз с минусом, успешно сокращаются. (Возможно, тут сокрыта какая-то вариация теоремы Карно).
Какая тут кажется может быть мораль? Надо бы придумать какое-то геометрическое объяснение формуле со скриншота. Мне кажется, не очень хорошей идея думать прямо про эту формулу и мне кажется, лучше из степени сделать линейную функцию. Для этого надо вычесть из нее что-то. Есть два хороших кандидата, которые приводят приблизительно к одному и тому же результату.
Первый кандидат — вычесть степень точки относительно какой-то окружности, проходящей через точки P и Q. Второй — вычесть степень точки относительно точки X.
В обоих случаях формула, которая получится, будет иметь вид
x= ... f(P) - ... f(Q)
Коэффициенты, обозначенные ... такие же как на скриншоте, относятся как (PX/QX)^2 и имеют разный знак, поэтому выражение сворачивается в формулу для f(O), где O — центр окружности Аполлония, построенной по точке X и отрезку PQ. (Кстати, у точки O степень относительно любой окружности, проходящей через P и Q как раз равна OX^2.)
На этом мысль у меня немного обрывается, но возможно, кто-то сможет предложить еще какую-то геометрическую идею, которая бы обяснила формулу и почему задача верна.
Ладно, вот вам другая задача. А то говорят мало задач про многоугольники))
Даны два правильных шестиугольника.
(a) Докажите, что сумма площадей красных четырехугольников равна сумме площадей синих.
(b) Докажите, что сумма квадратов площадей красных четырехугольников равна сумме квадратов площадей синих.
Авторы: Fotis Dellaportas
и В.Н. Дубровский
Даны два правильных шестиугольника.
(a) Докажите, что сумма площадей красных четырехугольников равна сумме площадей синих.
(b) Докажите, что сумма квадратов площадей красных четырехугольников равна сумме квадратов площадей синих.
Авторы: Fotis Dellaportas
и В.Н. Дубровский
Forwarded from Математические кружки | «МТ кружки»
Куда ж без геометрии? Четвёртая задачная разминка — от нашего преподавателя Бахарева Фёдора Львовича. Развёрнутое предисловие от автора:
На этой неделе я предлагаю вам порешать геометрические задачи, которые связывает то, что внутри некоторой фигуры располагается сразу несколько окружностей.
Первая задача (сравнительно простая) предлагалась 8-классникам в далёком 1986-м году на Всероссийской олимпиаде и недавно была предложена на олимпиаде «Высшая проба» в 10-м классе.
Вторая задача посложнее, она предлагалась в 1990-м году тоже на Всероссийской олимпиаде, но в 10-м классе.
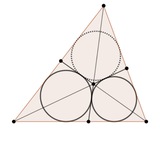
И, наконец, третья задача является классикой. Три окружности, расположенные внутри треугольника указанным образом, называются окружностями Мальфатти. Джанфранческо Мальфатти в 1803 году решал задачу построения трёх таких окружностей, будучи убеждённым, что именно такие три круга внутри треугольника занимают наибольшую площадь. (На самом деле он решал задачу высечения трёх круглых колонн наибольшего объёма из треугольной призмы мрамора). В 1967-м году оказалось, что окружности Мальфатти не только не решают задачу, но и не являются оптимальным решением ни для какого треугольника. Обе задачи — построения окружностей Мальфатти и вырезания трёх непересекающихся кругов максимальной площади — называются задачами Мальфатти.
Задача построения трёх касающихся окружностей внутри треугольника была предложена японским математиком XVIII века Адзимой Наонобу ещё до работы Мальфатти, и эта задача была включена в неопубликованную коллекцию работ Адзимы, собранную годом позже его смерти его учеником Кусакой Макото. Именно в честь двух этих математиков и названа точка пересечения, наличие которой надо установить в третьей задаче.
Будем рады решениям в комментариях! Пока это самая сложная наша разминка.
Разбор задач будет проводиться Фёдором Львовичем в субботу 20 апреля в 15:00 мск по ссылке https://us06web.zoom.us/j/5634707332?pwd=TUcxTlJQbmxxMGRucDJ0ejVDaVZ3UT09&omn=85978497498
Meeting ID: 563 470 7332
Passcode: 141592
Присоединяйтесь!
#мтразминка
На этой неделе я предлагаю вам порешать геометрические задачи, которые связывает то, что внутри некоторой фигуры располагается сразу несколько окружностей.
Первая задача (сравнительно простая) предлагалась 8-классникам в далёком 1986-м году на Всероссийской олимпиаде и недавно была предложена на олимпиаде «Высшая проба» в 10-м классе.
Вторая задача посложнее, она предлагалась в 1990-м году тоже на Всероссийской олимпиаде, но в 10-м классе.
И, наконец, третья задача является классикой. Три окружности, расположенные внутри треугольника указанным образом, называются окружностями Мальфатти. Джанфранческо Мальфатти в 1803 году решал задачу построения трёх таких окружностей, будучи убеждённым, что именно такие три круга внутри треугольника занимают наибольшую площадь. (На самом деле он решал задачу высечения трёх круглых колонн наибольшего объёма из треугольной призмы мрамора). В 1967-м году оказалось, что окружности Мальфатти не только не решают задачу, но и не являются оптимальным решением ни для какого треугольника. Обе задачи — построения окружностей Мальфатти и вырезания трёх непересекающихся кругов максимальной площади — называются задачами Мальфатти.
Задача построения трёх касающихся окружностей внутри треугольника была предложена японским математиком XVIII века Адзимой Наонобу ещё до работы Мальфатти, и эта задача была включена в неопубликованную коллекцию работ Адзимы, собранную годом позже его смерти его учеником Кусакой Макото. Именно в честь двух этих математиков и названа точка пересечения, наличие которой надо установить в третьей задаче.
Будем рады решениям в комментариях! Пока это самая сложная наша разминка.
Разбор задач будет проводиться Фёдором Львовичем в субботу 20 апреля в 15:00 мск по ссылке https://us06web.zoom.us/j/5634707332?pwd=TUcxTlJQbmxxMGRucDJ0ejVDaVZ3UT09&omn=85978497498
Meeting ID: 563 470 7332
Passcode: 141592
Присоединяйтесь!
#мтразминка