Четырехугольник ABCD вписаный, E — середина CD, P — точка пересечения диагоналей, Q — точка пересечения BC и AD. Точка F такова, что AEBF — гармонический четырехугольник. Докажите, что P, Q и F лежат на одной прямой.

Что-то на клоусонском...

Для тех, кто забыл, кто такой Клоусон. На самом деле это инверс-симметрия с центром в точке Микеля, освежающая немного понимание теоремы Клиффорда. Впервые на канале это появилось вот в этом видео: https://youtu.be/a0CqrAzJ54c?si=TAPYpYc8So6YiRRA

В треугольнике ABC проведены высоты AD, BE и CF, которые пересекаются в точке H. Середины отрезков AH, BH и CH соединили соответственно с центрами вписанных окружностей треугольников AEF, BFD и CDE. Докажите, что три указанные прямые пересекаются в одной точке.

Добрая задача про трапецию

кстати, если кто-то не понял, почему утренняя задача прикольная:

потому что указанные прямые пересекаются в точке Фейербаха. И хорошим подспорьем действительно служит понимание того, что точка Фейербаха это анти-Штейнер для прямой OI.

Продолжаем вчерашнюю тему. Точки касания вписанной окружности со сторонами треугольника отразили относительно прямой OI и соединили с соответствующими вершинами. Тогда полученные прямые пересекаются в одной точке, причем точка эта изогонально сопряжена точке Фейербаха.

Добрая задача про равные окружности: красные окружности равны, докажите, что угол прямой

В чате написали, что помимо элементарных решений задачи про красные окружности есть и неэлементарные.

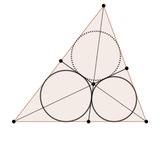
В верхней полуплоскости в модели Пуанкаре красные окружности - эквидистанты для прямой-окружности описанной вокруг пунктирного треугольника. Из-за маленьких окружностей эквидистанты на равном расстоянии от своей прямой, прямыми вычислениями можно проверить, что тогда и их евклидовые радиусы будут равны
(прямые вычисления проще сделать проведя

И комментарий от Павла Витальевича Бибикова:

Даже проще. Для двух окружностей-эквидистант их база - биссектриса внутреннего угла между ними, а абсолют - внешняя, т.к. база и абсолют перпендикулярны. И так, наверное, можно обобщить на случай неравных окружностей...

Кстати, самое время объявить, что мы с Павлом Витальевичем договорились о второй серии ликвидации безграмотности в области использования неевклидовых методов решения евклидовых геометрических задач. Вторая серия состоится, как и в прошлый раз, приблизительно в начале мая (анонс будет чуть позже, как и точное время и место). Но если вы хотите подготовиться к этому мероприятию, то есть смысл посмотреть и осознать первую серию.

https://www.youtube.com/live/TDU0JB_YDnw?si=942UV-YLm34Zpe5L

Сербская национальная олимпиада 2024, задача 4.

Опять задача про Шалтая и Болтая. Закрашенный четырёхугольник является параллелограммом.

Еще одна добрая задача

Дабромат в Калининграде

Преподаватели Дабромат вернулись с выездной школы, организованной Центром развития одаренных детей в Калининграде. По итогом работы мы сверстали небольшую книжечку, состоящую из методических материалов, которые были использованы при обучении детей. Книжечку можно использовать при обучении и распространять в открытых источниках.

Текст был сверстан одним из преподавателей Дабромат, пока он перемещался между калининградскими и московскими сборами — в ней вполне могут быть опечатки. Писать о них можно прямо в комментариях к этому посту.

Дети на сборах были поделены на 4 группы, в зависимости от уровня знания геометрии. Материалы начинающей группы можно использовать при обучении семиклассников, тогда как задачи профи группы вполне подойдут для подготовки к финалу ВсОШ по математике. Многие задачи профи группы также были выданы на занятиях сборной Москвы в рамках тренировки перед финалом ВсОШ. А сможете ли вы осилить последнюю задачу? Пишите решения в комментариях!

Подписывайтесь на наш канал, чтобы не пропустить другие интересные материалы.

Добрая задача

Олимпиада 239, 2024, 8-9, задача 4

П.С. Просьба пока не обсуждать решение!

Касательную к вписанной окружности треугольника отразили относительно биссекстрис его внешних углов. Докажите, что три полученные прямые ограничивают треугольник, равный исходному.

По интересным траекториям ездят вершины, а инцентр ездит по окружности, описанной около IaIbIc

Добрая задача

Не очень добрая задача... в которой условие звучит как список основных замечательных точек треугольника...

I — центр вписанной окружности
O — центр описанной окружности
G — точка пересечения медиан
H — ортоцентр
F — точка Фейербаха
L — точка, симметричная H относительно O (называется точка де Лоншана)


Тогда точка F лежит на радикальной оси описанной окружности и окружности (IGL)