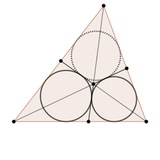
Республиканская олимпиада Казахстана, 2024, первый день, задача 9.3

В окружность omega с центром O вписан остроугольный неравнобедренный треугольник ABC. Точка M — середина стороны BC. Касательная прямая к omega в точке A пересекает сторону BC в точке D. Окружность с центром в точке M и с радиусом MA пересекает продолжения сторон AB и AC в точках K и L соответственно. Пусть X такая точка, что BX параллельно KM и CX параллельно LM. Докажите, что точки X, D, O лежат на одной прямой.

Красивая задача!

Всеукраинская олимпиада 9.4.

На боковых сторонах AC и AB равнобедренного треугольника ABC выбраны точки E и F соответственно так, что AE=BF. Точка D выбрана по ту же сторону от прямой EF, что и точка A, таким образом, что треугольники DFE и ABC подобны. Прямая EF пересекает прямую BC в некоторой точке K. Докажите, что прямая DK касается описанной окружности треугольника ABC.

Автор: Федир Михайлович Юдин.

Источник: https://tttttt.me/geometry_ukraine

На этой неделе на тренировках по геометрии Поворотная гомотетия и лемма о велосипедистах. Присоединяйтесь)

USAMO-2024, Problem 5
USAJMO-2024, Problem 6
Автор Антон Тригуб.

Точка D внутри треугольника ABC такова, что ∠DAC=∠ACB и ∠BDC=90°+∠BAC. Точка E выбрана на луче BD так, что AE=EC. Точка M — середина стороны BC. Докажите, что AB касается окружности, описанной около треугольника BEM.

Про точку Болтая от Ahmet Çetin

(Угадайте тему следующей тренировки 🤣)

Чуть менее загадочное, но не менее прекрасное того же автора

Ну и в завершении абсолютно безумный факт, который я узнал из чата этого канала от Кирилла Бельского.

Кстати, вы знаете, что угол OIH всегда больше 135 градусов? (это я узнал из книжки Седракяна)

ничего не понятно...

На ночь глядя...

https://youtu.be/EKypmxsUWDU

Три Шалтая, три Болтая, а середины лежат на одной прямой...

Дополнительный факт из чата (от Кирилла Бельского). Серединные перпендикуляры к отрезкам пересекаются в одной точке

Очередная задача от компьютера. Источник: 2022 Czech and Slovak Olympiad III. Закрашенный четырёхугольник является прямоугольником.

На этой неделе тренируемся задачами на точку Болтая

Доведіть, що червоні кути рівні 😳

O, I, N — центры описанной окружности, вписанной окружности и окружности девяти точек треугольника. Докажите, что отмеченные углы равны.

Сегодня на разборе задач про точки Болтая будем, в частности, обсуждать две задачи с довольно свежих олимпиад

Прямая Эйлера треугольника ABC отсекает от него треугольник ADE. Тогда оказывается прямая Эйлера треугольника ADE параллельна стороне BC.

На следующей тренировке про Симсона и Штейнера будем думать...