По мотивам вчерашнего прорешивания

Шедевр Алексея Доледенка с только что прошедшей ММО. На мой взгляд, пока что это лучшая задача сезона и лучшая геометрия ММО со времен звезды Кушнира.

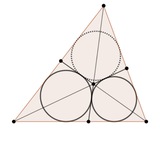
Серые отрезки высоты, зеленые — биссектрисы понятно чего. Найдите сумму красных углов.

Так и не понял, какое отношение эта задача имеет к задаче с заочного тура олимпиады Шарыгина. Ф — точка Фейербаха треугольника.

На сайте олимпиады Шарыгина появились официальные решения заочного тура!

В 11-ой задаче решения явно более простое, чем у меня 🤣

Да и в 10-ой... хотя про 10-ую я даже не уверен, что у меня правильное решение...

В 20-й тоже более изящное наблюдение, конечно)

https://geometry.ru/olimp/2025/2025_zaoch_sol_rus.pdf

Теорема Дезарга = Теорема Паскаля.
Хотим например доказать теорему Дезарга для выделенных цветных треугольников. Тогда по обратной теореме Паскаля получаем, что красные точки на одной конике. Применяя теорему Паскаля для них, но в другом порядке получаем нужную коллинеарность.

USAMO-2025, P4.

Кажется, у меня практически эта задача была в листочке пару недель назад... 😂

Это автор канала с недоумением смотрит в будущее и обсуждает на Сириус-курсах, какие задачи через три года будут на USAMO

Мне нравится такая задача.

Педальные треугольники точек P и Q подобны естественным образом. Докажите, что прямая PQ проходит через центр описанной окружности треугольника!

// к дню рождения А.А.Заславского

https://turgor.ru/problems/46/vs-46-baz-avt.pdf
https://turgor.ru/problems/46/vs-46-sl-avt.pdf

опубликованы задачи весеннего Турнира городов

Олимпиада Эйлера - 2025, первый день, задача 2.

Докажите, что площади зеленых треугольников равны.

в новый Квант (№2 за 2025 год) вошла статья Ф.Бахарева и Г.Челнокова про Why-точки, полуописанные окружности и прямую Эйлера

https://biblio.mccme.ru/node/281875

ранее на эту тему: https://tttttt.me/olympgeom/1265

Точки P и Q изогонально сопряжены в треугольнике ABC, H — ортоцентр треугольника, AEPF — параллелограмм. Докажите, что если P лежит на (BHC), то QE=QF.

Точки P и Q изогонально сопряжены в треугольнике ABC. S — середина малой дуги BC окружности (ABC). R такая точка на окружности (BPC), что PR и AS параллельны. Докажите, что Q, R и S лежат на одной прямой.

Республиканская олимпиада Казахстана 2025

9 класс задача 4 (из 6). Автор М. Кунгожин

В неравнобедренном треугольнике ABC точка M — середина стороны AB, I — центр вписанной окружности, а J — середина дуги AB окружности, описанной около треугольника ABC, не содержащей точку C. К окружности с центром J и радиусом JM провели касательные IP и IQ (A и P лежат по одну сторону от прямой CI). Описанные окружности треугольников APJ и BQJ вторично пересекаются в точке R. Докажите, что R лежит на прямой AB.

ЗАДАЧИ И ИТОГИ УСТНОГО ТУРА — 2025

Сегодня, 30 марта в Москве состоялся заключительный устный тур 46го Турнира городов!

Опубликованы условия задач.

По итогам тура жюри приняло решение наградить
— дипломами I степени — участников, решивших не менее 4 задач (всего 25 человек);
— дипломами II степени — участников, решивших 3 задачи (всего 24 человека).
— дипломами III степени — участников, решивших 2 задачи (всего 56 человек).

Жюри также отмечает похвальными грамотами участников, решивших одну задачу.

#устныйтур

По просьбам особо активных участников выкладываю условия олимпиады 239. Довольно во многих питерских кружках принято задачи олимпиады выдавать в качестве серии, поэтому просьба в чате не обсуждать решения как минимум в ближайшие несколько дней.

на картинке есть правильная пятиконечная звезда, но найти ее не так просто...

Можно ли с помощью одной линейки установить, являются ли две данных окружности концентрическими?